 Witam
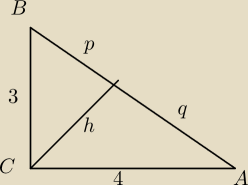
Witam  Mam takie oto zadanie: W trójkącie prostokątnym o przyprostokątnych długości 3 i 4
poprowadzono wysokość z wierzchołka kąta prostego. Oblicz długość odcinków, na jakie
wysokość ta podzieliła przeciwprostokątną.
Zadanie jest samo w sobie banalne, ale potrzebuję więcej sposób rozwiązania, a mi już
się mózg roztopił nad tym trójkątem.
Na razie zrobiłam takie:
1) W trójkącie ACD, że przeciw prostokątna 42 = h2 + q2 i w ten sam sposób w trójkącie CBD,
9= h2 + p2, no i że h2 = p*q i że p+q=5, itd.
2) Tu mam, że pole ABC = 0,5 * 5*h = 0,5 *3*4, potem z tego h i znowu, h2 = p*q i p+q=5, no
i
potem policzyłam p i q z funkcji kwadratowej
3) Narysowałam ten trójkąt w układzie równań, wyznaczyłam równanie prostej przechodzącej przez
AB, potem równanie prostopadłej do niej przechodzącej przez CD ( h ), wyznaczyłam punkt D
i wersja pierwsza − policzyłam długość odcinka AD, wersja druga − poprowadziłam wysokość na AC
i z podobieństwa trójkątów policzyłam długość AD.
No i wyczerpały mi się pomysły, a potrzebuję jeszcze przynajmniej 1, najlepiej byłoby więcej
<prosi
Mam takie oto zadanie: W trójkącie prostokątnym o przyprostokątnych długości 3 i 4
poprowadzono wysokość z wierzchołka kąta prostego. Oblicz długość odcinków, na jakie
wysokość ta podzieliła przeciwprostokątną.
Zadanie jest samo w sobie banalne, ale potrzebuję więcej sposób rozwiązania, a mi już
się mózg roztopił nad tym trójkątem.
Na razie zrobiłam takie:
1) W trójkącie ACD, że przeciw prostokątna 42 = h2 + q2 i w ten sam sposób w trójkącie CBD,
9= h2 + p2, no i że h2 = p*q i że p+q=5, itd.
2) Tu mam, że pole ABC = 0,5 * 5*h = 0,5 *3*4, potem z tego h i znowu, h2 = p*q i p+q=5, no
i
potem policzyłam p i q z funkcji kwadratowej
3) Narysowałam ten trójkąt w układzie równań, wyznaczyłam równanie prostej przechodzącej przez
AB, potem równanie prostopadłej do niej przechodzącej przez CD ( h ), wyznaczyłam punkt D
i wersja pierwsza − policzyłam długość odcinka AD, wersja druga − poprowadziłam wysokość na AC
i z podobieństwa trójkątów policzyłam długość AD.
No i wyczerpały mi się pomysły, a potrzebuję jeszcze przynajmniej 1, najlepiej byłoby więcej
<prosi  >
p = 16/5
q = 9/5
P.S wiem, ze lepiej jakbym zapisała równania itd. bo byłoby łatwiej zobaczyć o co mi chodziło w
tych sposobach, ale ja nie znoszę pisać liczb itd. na klawiaturze...
>
p = 16/5
q = 9/5
P.S wiem, ze lepiej jakbym zapisała równania itd. bo byłoby łatwiej zobaczyć o co mi chodziło w
tych sposobach, ale ja nie znoszę pisać liczb itd. na klawiaturze... 

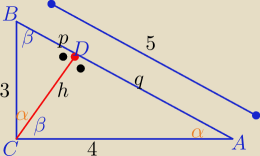 Dwa takie sposoby:
Dwa takie sposoby:
| a*b | 12 | |||
1/ |AB|=5 ⇒ p+q=5 , h= | = | |||
| c | 5 |
| h | 3 | 4 | 12 | 16 | 16 | 9 | ||||||||
= | ⇒ q= | * | = | to x= 5− | = | |||||||||
| q | 4 | 3 | 5 | 5 | 5 | 5 |
| a2 | b2 | a2 | 9 | b2 | 16 | |||||||
+ | =c ⇒ p= | = | , q= | = | ||||||||
| c | c | c | 5 | c | 5 |