Wzory redukcyjne
Ania: α∊(90,180)
α=?
14 maj 18:27
14 maj 18:28
Nieuchwytny: t=sinα
(16)
−1/4=t
(2
4)
−1/4=t
t=2
−1
14 maj 18:31
Ania: | | 1 | |
No i teraz trzeba obliczyć α, do |
| sama doszłam  |
| | 2 | |
| | 1 | |
sinα= |
| ⇒ α=30 a skoro α∊(90,180) to musimy dodać 90. Wychodzi α=120, w odpowiedziach jest |
| | 2 | |
150. O co chodzi?
14 maj 19:35
Ania: Jest tu ktoś?
14 maj 20:01
Mila:
| | π | | 5π | |
α= |
| nie odpowiada warunkom zadania lub α= |
| |
| | 6 | | 6 | |
14 maj 20:07
Ania: A skąd się tu nagle π wzięło?
14 maj 20:21
zombi: π=180
o 
14 maj 20:22
Mila:
W której klasie jesteś? Nie wiem jaki miałaś materiał?
14 maj 20:33
Nieuchwytny:
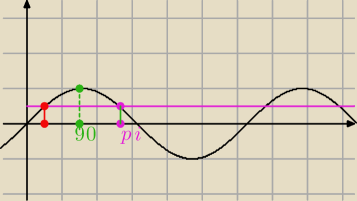
14 maj 20:33
Ania: 1 liceum, to jest wstęp do trygonometrii − wzory redukcyjne, podstawowe wartości sinusów.
14 maj 20:37
Mila:
W takim razie patrz do tabelki.
Masz wzór :
sinα=sin(180−α)
α=30
0 kąt I ćwiartki
sin30
o=sin(180−α)=sin(150
o)
14 maj 20:41
14 maj 20:43
Ania: Fakt, gdybym dodała 90 to by się zmieniło na cosinusa... Dopiero wszystko układam w głowie,
bardzo wszystkim dziękuję

14 maj 20:45
Mila:
Dobrze.

14 maj 20:47




