Wykaż
baśka: 1. W trójkącie prostokątnym ABC, w którym kąt C=90 poprowadzono odcinek CD w taki sposób, że
D∊AB oraz kąt BCD=2ACD. Wykaż, że jeżeli pola trójkątów ADC i BCD są równe, to kąty ostre
trójkąta ABC mają miarę 30 i 60.
14 maj 18:13
Nieuchwytny: Rysunek zrób

14 maj 18:21
baśka:
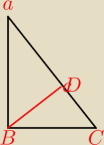
14 maj 18:28
Marcin: kąt C=90
o − popraw rysunek

14 maj 18:29
baśka: schematycznie oczywiście

14 maj 18:30
baśka:
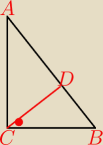
14 maj 18:31
baśka: wiem ,że α jest równa 30 stopni

bo 90 stopni =3α
14 maj 18:32
Nieuchwytny: Tego nie wiesz, to masz wykazać

14 maj 18:35
baśka: więc pomóż

14 maj 18:38
52:
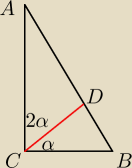
14 maj 18:45
baśka: i już?
14 maj 18:51
Nieuchwytny: PDCB=PADC
14 maj 18:58
52: Dobra, widzę że ci to opornie dosyć idzie
Przyrównujemy pola
| 1 | | 1 | |
| sinα*CD*BC= |
| sin2α*CD*AC |
| 2 | | 2 | |
sinα*BC=sin2αAC
α=30
o (tak jak napisałeś to wcześniej)
BC=
√3AC
Niech BC=a
14 maj 19:01
52:
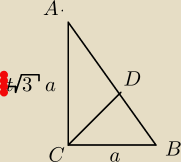
Teraz tw.pitagorasa
a
2+(a
√3)
2=AD
2
a
2+3a
2=AD
2
4a
2=AD
2
AD>0
AD=2a
14 maj 19:03
52:
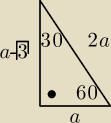
Jak się uczyłaś to wiesz, że...
14 maj 19:05
baśka: tak

Dzięki

14 maj 19:15
Marcin: 52, ale chyba |AB|=2a

14 maj 19:17
52: Tak przeoczenie moje. Marcin ma racje, powinno być AB zamiast AD
14 maj 19:18
Krzysztof: Inne rozwiązanie

20 kwi 20:42





 bo 90 stopni =3α
bo 90 stopni =3α



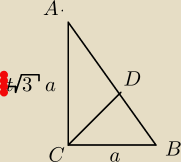 Teraz tw.pitagorasa
a2+(a√3)2=AD2
a2+3a2=AD2
4a2=AD2
AD>0
AD=2a
Teraz tw.pitagorasa
a2+(a√3)2=AD2
a2+3a2=AD2
4a2=AD2
AD>0
AD=2a
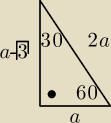 Jak się uczyłaś to wiesz, że...
Jak się uczyłaś to wiesz, że...
 Dzięki
Dzięki 

