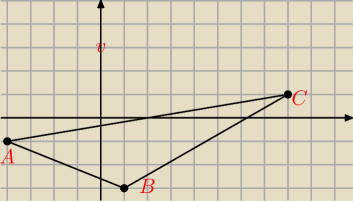
wysokość trójkąta malinka: Dane są wierzchołki A=(−4,−1) B=(1,−3) oraz C=(8,1). Oblicz długość wysokości opuszczonej z wierzchołka B oraz pole tego trójkąta.

J: 1) Równanie prostej AC 2) Równanie prostej prodtopadłej do AC przez punkt B 3) Punkt przecięcia tych prostych (D) 4) długośc IBDI = h

	1
5) Pole trójkata P=		IACI*h
	2

Marcin: Wyznacz równanie prostej zawierającej boki A i C, później policz odległość punktu B od tej prostej.

J: ....punkty A i C ..

Marcin: Punkty, punkty

52:

	1
1.PABC=		|(xB−xA)((yC−yA)−(yB−yA)(xC−xA)|
	2

2.Obliczasz długość odcinka |AC|, gdzie |AC|=√(x_C−x_A)² + (y_C−Y_A)²

	1
3.PABC=		*|AC|*h , oblicz z tego h
	2