Równanie z wartością bezwzględną Radek: Równanie z wartością bezwzględną. |x−2|=7−|x+5| |x−2|+|x+5|=7 Rozwiązuje przedziałami najpierw dla x(−∞,−5) x−2<0 x+5 i właśnie jakie wartości przyjmuje ? Bo dla −4=1 Dziękuje za pomoc

Tadeusz: Przedziałów będziesz miał trzy (−∞, −5) <−5, 2) <2, ∞)

Radek: No tak i najpierw rozwiązuje dla tego pierwszego i mam problem x−2<0 więc |x−2|=−x+2 x+5 i właśnie jakie wartości przyjmuje ? Bo dla −4=1

Tadeusz: 1^o x∊(−∞, −5) −x+2−x−5=7 ⇒ −2x=10 ⇒ x=−5 Rozwiązaniem w tym przedziale jest zbiór pusty

Tadeusz: 2^o x∊<−5, 2) x+5−x+2=7 ⇒ 7=7 czyli

bezendu: Czyli należy cały przedział

pigor: ... lub z interpretacji wartości bezwzględnej na osi Ox jako, że |x−a|=AB , to odległość punktów A=x i B=a masz: |x−2|+|x+5|=7 ⇔ −5≤ x ≤2 ⇔ x∊<−5;2> − rozwiązanie ...

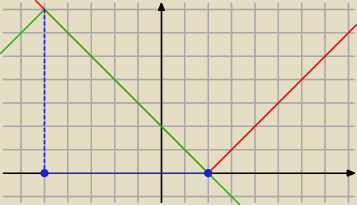
Marcin: Lub graficznie

Radek: Czyli x+5>0 ?W przedziale (−∞, −5) ?

ZKZ: Nie . masz |x+5| i przedzial (−oo,−5) wiec bierzemy jakaolwiek liczbe z tego przedzialu(nie krance np x=−10 i wstawiamy za x |−10+5|=|−5| wiec zgodnie z definicja wartosci bezwzglednej zmieniamy znak na przeciwny i tym przedziale |x+5|=−(x+5)=−x−5

Radek: A jak wezmę −4 to mam |−4+5|=1 więc jak to jest ?

Martiminiano: Ja tego typu zadania zawsze robię w ten sposób: |x−2|+|x+5|=7 x−2=0 i x+5=0 x=2 x=−5 więc, R=(−∞;−5)u<−5;2>u(2;+∞) Dla x∊(−∞;−5) Dla dowolnego x z tego przedziału pierwsza i druga wartość bezwzględna <0 więc −x+2−x−5=7 −2x=10 x=−5 , który nie należy do tego przedziału więc w tym przedziale nie mamy rozwiązań. Później robię analogicznie z 2 i 3 przedziałem. Jak dla mnie ten sposób jest najbardziej przejrzysty (oczywiście to subiektywna ocena).