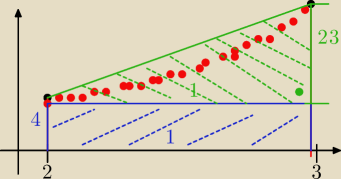
calki zadanie: Udowodnic nastepujace oszacowanie:

19		65
	<∫23 xxdx<		Wskazówka: Oszacowac xx przez xa.
3		4

ja zrobilem tak: f(x)=x^x=e^xlnx ; [2,3] f'(x)=e^xlnx*(lnx+1) >0 ; f rosnaca f''(x)>0 ; f wypukla f(2)=4 f(3)=27

	1		23
pole trojkata prostokatnego P=		*1*23=
	2		2

pole prostokata P=1*4=4

23		31		62		65
	+4=		=		<
2		2		4		4

	65
stad wynika, ze ∫23 xx dx<
	4

	19
ale nie wiem jak uzasadnic nierownosc		<∫23 xxdx
	3

podanej wskazowki nie rozumiem wiec zrobilem na rysunku ale drugiej czesci nie umiem moge prosic o pomoc?

PW: W gruncie rzeczy mogłeś oszacować x² < x^x < x³, po scałkowaniu otrzymasz obie nierówności. Ale sposób z funkcją wypukłą i oszacowaniem przez liniową podoba mi się.

zadanie: dziekuje

zadanie: obliczyc pole powierzchni powstałej przez obrót krzywej y =f(x) wokół osi OX. f(x)=√x ; [0,4]

	1
f'(x)=
	2√x

wzor: P=2π∫_a^bf(x)√1+(f'(x))²dx ale wtedy metoda podstawiania w granicach wyjdzie zero w mianowniku czy dobrze mysle?

zadanie: ?

zadanie: czy jakis inny sposob aby to obliczyc?

Mila:

	2		2
∫√x*√1+(1/4x) dx=∫√x+0.25 dx=		(x+0,25)32=		*(x+0,25)√x+0,25
	3		3

Dalej licz

zadanie: czyli

	2		17		17		1		1		17√17−1		1
2π(		*		√		−		√		)=2π(		)=		(17√17−1)π
	3		4		4		6		4		12		6

Mila: Tak.

zadanie: dziekuje

Mila: Jak z przygotowaniem do sesji?

zadanie: mam jeszcze problem z takim zadaniem Obliczyc objetosc bryły powstałej przez obrót obszaru arctgx ≤y≤√arctg²x+√1+sinx ; 0≤x≤π wokół osi OX . wzor na objetosc znam ale nie wiem na czym polega rozumowanie w tym zadaniu moge prosic o pomoc?

zadanie: sesja juz za miesiac powoli sie ucze

Mila: Od objętości bryły powstałej z obrotu krzywej y=√artg²x+√1+sinx odejmij objętość bryły powstałej przez obrót krzywej y=artgx wokół OX.