Pomocy! Natii: Jakieś pomysły? Z1. Obwód wycinka koła jest równy 2p. Wyznacz promień tego koła, wiedząc, że pole wycinka jest największe z możliwych. odp. p/2 Z2. W trójkąt T o kątach: α, β, π − α − β wpisano okrąg O o promieniu r. Wyznacz pole trójkąta, którego wierzchołkami są punkty styczności trójkąta T i okręgu O. odp. P = (1/2) r² * (sin α + sin β + sin (α + β))

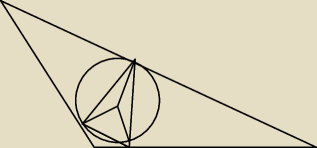
Mariusz95: Z2 przedstaw pole trójkąta jako sume pól trzech trójkątów powstałych w wyniku podzielenia trójkąta promieniem r a następnie

	1
Pole każdego z trójkątów policz za pomocą wzoru P=		absinα a=b=r
	2

Mariusz95: promienie są prostopadłe do boków trójkąta więc kąty pomiędzy ramionami będą równe 180−α 180−β oraz α+β

Natii: Dzięki!

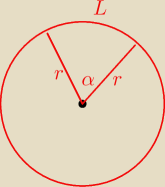
Janek191: z.1 2 p = 2 r + r α; L = α* r, α − miara w radianach

	2p − 2 r
więc r α = 2p − 2 r ⇒ α =
	r

oraz

	2p − 2 r
Pw = 0, 5 r2*α = 0,5 r2*		= − r2 + p r
	r

czyli P_w( r) = − r² + p r

	− p
Ta funkcja przyjmuje największą wartość dla r =		= 0,5 p
	2*(−1)

Eta: Ciągle te "klony" ( w jakim celu?

Natii: Dziękuję bardzo!