okrąg wpisany w trójkąt maturzysta: Oblicz pole koła wpisanego w trójkąt prostokątny, wiedząc że wysokość tego trójkąta opuszczona z wierzchołka kąta prostego dzieli przeciwprostokątną na odcinki długości 2 i 6. Poproszę o wskazówki jak to zrobić.

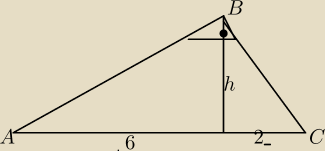
5-latek: Z twierdzenia o wysokosci opuszconej z wierzcholka kata prostego w trojkacie prostokatnym mamy h=√2*6=√12= 2√3 Z twierdzenia Pitagorasa oblicz teraz dlugosc odcinkow AB i BC AC=8

	1
Ptr=		AC*h
	2

teraz nastepny wzor P_tr= p*r gdzier p− polowa obwodu (a mozesz juz policzyc i r− promien okregu/kola wpisanego w trojkat i wylicz z niego r