Algebra Liniowa
Kojotek: Mam wybrakowane notatki i nie mogę przypomnieć sobie metody rozwiązywania takich równań
259x − 203y = 14
12 maj 15:50
marzenka: aby rozwiazać równanie z dwoma niewiadomymi trzeba mieć dwa równania
12 maj 15:52
kamczatka: masz tutaj dwie niewiadome x i y więc musisz mieć drugą równość np.
259x − 203y = 14
200x − 101.5 = 28
12 maj 15:53
PW: To jest równanie diofantyczne?
12 maj 15:53
Kojotek: Przedmiot nazywa się algebra liniowa dla informatyków, mieliśmy ten materiał krótko przed
kongluencjami.
12 maj 15:56
Janek191:
37 x − 29 y = 2
Poczytaj o równaniach diofantycznych

12 maj 15:58
Marcin:
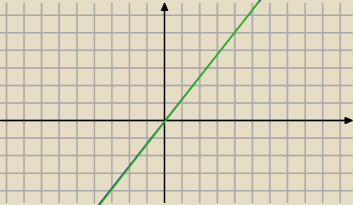
203y=259x−14 / :203
Kazdy punkt z tej prostej jest rozwiązaniem

12 maj 15:59
Janek191:
Raczej przed kongruencjami

12 maj 16:01
PW: No to na pewno idzie o równanie diofantyczne − szukamy rozwiązań (x,y) tego równania, które są
parami liczb całkowitych.
12 maj 16:01
Janek191:
Raczej przed kongruencjami

12 maj 16:03
PW: Cześć, Janek, widzę że komputer "się międli" i nie sygnalizuje poprawnie wysłania
odpowiedzi.
12 maj 16:09
Kojotek: Okej, to jest równanie diofantyczne i z notatek kolegi ( również wybrakowane :< ) wynika, ze do
rozwiązania były wykorzystywane macierze i NWD. Ale zupełnie nie widzę tu żadnych zależności
ani logiki. Może ktoś domyśla się o co chodzi? Jestem już całkiem załamany.
12 maj 16:28
Janek191:
37 x − 29 y = 2
Mamy
x
0 = 22 , y
0 = 28
bo 37*22 − 29*28 = 814 − 812 = 2
oraz wszystkie rozwiązania dane są :
x = x
0 + b
1*t = 22 + 29 t
y = y
0 − a
1* t = 28 + 37 t
t − dowolna liczba całkowita
gdzie
a = 37
b = − 29
| | a | |
a1 = |
| = − 37 |
| | NWD( 37, −29) | |
| | b | |
b1 = |
| = 29 |
| | NWD( 37, − 29) | |
12 maj 16:30
Janek191:
Są to równania nieoznaczone pierwszego stopnia o dwóch niewiadomych.
patrz: Wacław Sierpiński − Wstęp do teorii liczb WSiP W− wa 1987 s. 18 − 19
12 maj 16:33
Janek191:
259 x − 203 y = 14 / : 7
37 x − 29 y = 2
itd. jak wyżej

12 maj 16:36
Janek191:
Jak wyznaczyć x
0 i y
0 ?
Np.
37 x − 29 y = 2
29 y = 37 x − 2
Wstawiamy kolejne liczby naturalne za x , aż otrzymamy liczbę y − będącą liczbą naturalną
lub całkowitą.
Dla x
0 = 22 wyszło y
0 = 28
12 maj 16:41
Janek191:
Co z Kojotkiem ?

12 maj 16:42
Kojotek: x0 i y0 dałem radę z tych macierzy już wyznaczyć, po twoim uzupełnieniu już wszystko wiem!
Dziękuję
12 maj 16:59

 203y=259x−14 / :203
203y=259x−14 / :203




