granice zadanie: Obliczyc granice (wykorzystujac calki oznaczone) 1)

	1		1		1		1		1
lim		+		+		+		+...+
	n		n+1		n+2		n+3		2n

n→∞ moglbym prosic o pomoc? nie za bardzo wiem jak wykorzystac tu calki?

Krzysiek: 0=x₀<...<x_k<...<x_n=1 k=0,...,n x_k=k/n, Δx_k=1/n f(x_i)=1/(1+i/n) , i=1,...,n (x_i−prawy koniec przedziałów [x₀,x₁], ...,[x_n−1,x_n] ) f(x)=1/(1+x)

	1		1
=lim 1/n (		+...+		)=
	1+1/n		1+n/n

	1
=lim 1/n∑i=1n		=∫011/(1+x)dx=ln2
	1+i/n

zadanie: dziekuje

zadanie: a ten przedzial to dlaczego jest od 0 do 1? z czego to wynika?

Krzysiek: masz przedział [0,1] dzielisz go na 'n' części i każda z nich ma długość Δx_k=1/n

	1
więc jak masz lim 1/n ∑in		=lim 1/n∑i=1nf(xi)=∫01f(x)dx
	1+i/n

a czemu taki przedział i z czego to wynika? z zadania. patrzysz na x_i=i/n czyli x_n=1 (to jest prawy koniec przedziału ) x₁=1/n (ale to też jest prawy koniec przedziału o długości 1/n, więc lewy to 0 ) więc masz przedział [0,1]

zadanie: dziekuje mam jeszcze takie pytanie:

	k(b−a)
do czego stosuje sie taki wzor w calkach: a+		?
	n

do podzialu przedzialu na n rownych czesci?

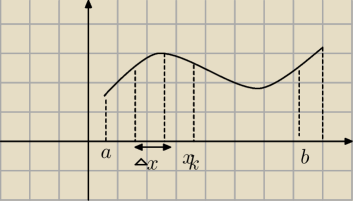
Krzysiek: przecież to żaden wzór... jak masz przedział [a,b] dzieląc na 'n' równych części przedziały będą mieć długość Δx=(b−a)/n x₀=a x₁=a+Δx x₂=a+2Δx ...

	b−a
xk=a+k*Δx=a+k*
	n

zadanie: dziekuje