Równania Lukas: Jestem tegorocznym maturzystą poziom P Rozwiąż równanie (cosx + sin x)²−2sinxcosx=2sinx , wiedząc, że x jest kątem ostrym.

	1
sinx=
	2

	π
x=		+2kπ
	6

Czy tak to nalży rozwiązać ?

Eta: Dla kątów ostrych x∊(0,90^o)

	1
sinx=		⇒ x=30o
	2

Lukas: A nie należy tego brać z tablic ?

Eta:

	1
Myślę,że wiesz ,że sin30o=		( w tablicach masz zapisaną tę samą wartość
	2

Lukas:

	π
Tak, mam napisaną wartość. A czy podanie		jest błędem ? Pytam bo muszę nadrobić R i chcę
	6

dobrze zacząć od początku

Eta:

	π
30o=		rd ( radianów więc możesz też tak zapisać
	6

Lukas: Dziękuję, a mogę mieć jeszcze dać kilka przykładów ?

Lukas:

	cos3α+sin2αcosα
Wyznacz miarę kąta ostrego α , dla którego wyrażenie		ma wartość 2
	cos2α

Czy tutaj nie trzeba ustalać dziedziny ? cos²α≠0 ?

Lukas: ?

Piotr 10: Oczywiscie, ze trzeba ustalic dziedzine cos2α≠0

Marcin:

cos3x+(1−cos2x)cosx
	=2
cos2x

cos³x+(1−cos²x)cosx=2cos²x cos³x+cosx−cos³x=2cos²x cosx=2cos²x 2cos²x−cosx=0 Dziedzina to wiadomo.

Lukas:

	π
x≠		+kπ
	2

cosx(2cosx−1)=0

	1
cosx=0 lub cosx=−
	2

i zero odpada a to drugie jak rozwiązać ?

pigor: , tak , możesz ale (ja robię, bo lubię rozwiązywać metodą równań równoważnych), .. nie musisz, wtedy musisz (... powinieneś) zanim podasz odpowiedź zrobić sprawdzenie, czy L=P twojego równania dla każdego znalezionego rozwiązania x (mnie tego nie chce się robić. dlatego wolę zawsze − no, prawie zawsze) podać D równania ... ;

Lukas: Mogę liczyć na wskazówkę ?

Eta: cosx≠0

cosx(cos2x+sin2x)		1		1
	=2 ⇒		=2 ⇒ cosx=		⇒x=60o
cos2x		cosx		2

Lukas: To gdzie ja popełniłem błąd kończąc sposób Marcina ?

Eta:

	1
2cosx−1=0 ⇒ 2cosx=1 ⇒ cosx=+
	2

Lukas: Dziękuję ślicznie

Lukas:

	1
A jak rozwiązać przykład gdy mam sinx=−		?
	2

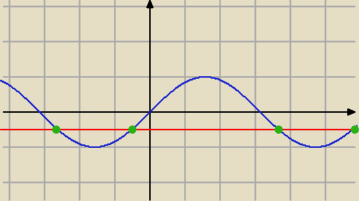
Marcin: Rysyjesz sinusoide i z niej odczytujesz rozwiązania

pigor: ... lub wiesz − jak sądzę , że sin30^o=sin^π₆=¹₂, więc mówisz sobie gdzie sinus jest ujemny (np. z wierszyka − tabelki III i IV ćw.) lub z wykresu, który masz "w głowie" i piszesz : x= −^π₆+2kπ v x= π+^π₆+2kπ= ⁷₆π+2kπ , k∊C. ..