Liczby -4 i 2 sa liczbami zerowymi funkcji kwadratowej f(x)= x^2 + bx + c. Podaj LuKeT: Liczby −4 i 2 sa liczbami zerowymi funkcji kwadratowej f(x)= x² + bx + c. Podaj zbiór argumentów, dla których f(x) <−8

Saizou : f(x)=(x+4)(x−2)<−8

Janek191: f(−4) = 0 i f(2) = 0 więc (−4)² − 4 b + c = 0 2² + 2b + c = 0 Rozwiąż układ , a następnie wstaw za b i c do f Rozwiąż nierówność f(x) < − 8

Alexy: Cześć, mam identyczne zadanie, ale: @Saizou: rozwiązałem i co dalej @Janek191: nie za bardzo wiem o co Ci chodzi. 16 − 4b + c = 0 4 + 2b + c= 0

Saizou : jak to rozwiązałeś to masz już zbiór argumentów Janek191 proponuje układ równań, bo jeśli liczby −4 i 2 są miejscami zerowymi f(x), to f(−4)=f(2)=0

Alexy: Dla pewności podam wynik f(x)=x²+2x−8<−8

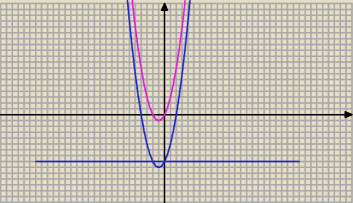
Janek191: Trzeba wyliczyć b i c : Odejmujemy stronami 12 − 6 b = 0 b = 2 c = − 4 − 2b = − 4 − 4 = − 8 więc f(x) = x² + 2 x − 8 Nierówność f(x) < − 8 czyli x² + 2 x − 8 < − 8 x² + 2x < 0 x*( x + 2) < 0 x₁ = − 2, x₂ = 0 Ramiona paraboli o równaniu y = x² + 2x = x*( x + 2) są skierowane do góry, zatem x ∊ ( x₁; x₂) = ( − 2 ; 0) =================== Sposób Saizou jest krótszy ! Dodatkowo − rysunek

Alexy: Jest to dobrze wykonane i taką mam podać odpowiedź?

LuKeT: Dzięki moi mili, Saizou właśnie w ten sposób kombinowałem, tylko wydawało mi się, że czegoś jeszcze nie napisałem. Janku; czy przy odpowiedzi konieczne jest uwzględnienie tego x ∊ ( x1; x2) = ( − 2 ; 0)