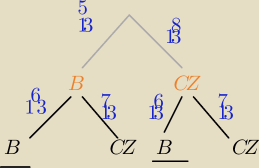
mózgi letsgo: Zadanie dla mózgów z probabilistyki Z pierwszego pudełka, w którym znajduje się pięć kul białych i osiem kul czarnych, losujemy jedną kulę i przekładamy ją do drugiego pudełka, w którym początkowo znajdowało się sześć kul białych i siedem kul czarnych. Po wymieszaniu kul w drugim pudełku losujemy z niego jedną kulę. Oblicz prawdopodobieństwo, że z drugiego pudełka wylosujemy kulę białą.

letsgo: chodzi mi o sprawdzenie drzewka i tyle

letsgo: poprawiłem

letsgo: chyba źle

PW: W ogóle te drzewka nie odzwierciedlają treści zadania. Po co te "lewe" gałęzie? Przecież takie zdarzenia nie mają miejsca − te odpowiadające gałęziom

	5		7
		−−−		.
	13		14

letsgo: Co w takim razie radzisz mi?

PW: Przestań rysować drzewka. Zapoznaj się z twierdzeniem o prawdopodobieństwie całkowitym. W tym zadaniu przestrzeń zdarzeń Ω składa się z dwóch rozłącznych zbiorów B₁ i B₂ (dwóch różnych urn przygotowanych do drugiego losowania).

	5
P(B1) =
	13

	8
P(B2) =		.
	13

Prawdopodobieństwa tych zbiorów były zaszyfrowane w treści zadania w postaci prostego zadania o losowaniu jednej kuli z urny zawierającej 13 kul. Zdarzenie A − wylosowano białą kulę" zgodnie z twierdzeniem o prawdopodobieństwie całkowitym ma prawdopodobieństwo określone wzorem: P(A) = P(A|B₁)•P(B₁) + P(A|B₂)•P(B₂).

	7		6
Prawdopodobieństwa P(A|B1) i P(A|B2) liczymy w pamięci P(A|B1)=		i P(A|B2)=
	14		14

(można je zapisać na początku rozwiązania jako założenia wynikające z treści zadania).

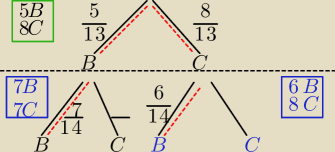
Mila: Po losowaniu kuli z pierwszego pudełka i dołożenia tej kuli do drugiego, mamy w drugim pudełku: (7B,7C) albo (6B,8C) A− wylosowano białą kulę z drugiego pudełka

	5		7		8		6		83
P(A)=		*		+		*		=
	13		14		13		14		182

letsgo: PW dzięki, daje mi to do myślenia. Duża wiedza, to też duża odpowiedzialność . Mila, również za zainteresowanie tematem.