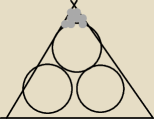
Pole wycinka trójkąta równobocznego Patryk: Dany jest trójkąt równoboczny o boku mającym długość a. W ten trójkąt wpisano trzy okręgi o równych promieniach w taki sposób, że każdy okrąg jest styczny do dwóch boków trójkąta i pozostałych dwóch okręgów (zobacz rysunek). Wyznacz – w zależności od a – pole figury zaznaczonej kolorem szarym. ( Przepraszam za rysunek)

qwe: dołączam się do pytania

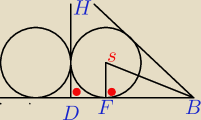Nieuchwytny: Z podobieństwa trójkątów obliczysz r. HDB, SFB

Janek191:

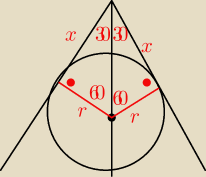
	x
Mamy		= tg 60o = √3 ⇒ x = √3 r
	r

oraz 2r + 2 x = a 2 r + 2*√3 r = a ( 2 + 2√3) r = a

	a		a2		a2
r =		⇒ r2 =		=
	2 + 2√3		4 + 8√3 + 12		16 + 8√3

P = 2*P₁

	1		1
P1 = 0,5 x*r −		π r2 = 0,5*p{3]*r*r −		π r2 =
	6		6

	1		a2
= [ 0,5 √3 −		π ]*
	6		16 + 8√3

zatem

	1		a2
P = 2 P1 = [ √3 −		π]*
	3		16 + 8√3

=============================

Patryk: Dzięki Janek191, jesteś Wielki

5-latek: Pewnie tak . BO ma okolo 2 m wysokosci

Janek191: Tylko 184 cm

5-latek: No to ja jestem o 10cm nizszy wiec jestes i tak wyzszy

wiktor: tak z ciekawosci z jakiej to ksiazki zadanie ?