Geometria płaska - trójkąty twierdzenie o stycznej i siecznej
Lili:
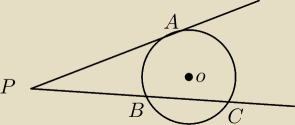
Z punktu P poprowadzono styczną w punkcie A do okręgu o środku O oraz sieczną przecinającą
okrąg w punktach B i C (rysunek)
Wiedząc, że |PC|=25 ,|CO|=15, |OP|=17. Oblicz |PA|, |PB|
Bardzo proszę o pomoc, jakąkolwiek wskazówkę w jakim kierunku powinnam iść
11 maj 15:03
Janek191:
Z odpowiedniego twierdzenia mamy:
I PB I *I PC I = I PO I2 − r2
więc
I PB I * 25 = 172 − 152 = 289 − 225 = 64
I PB I = 64 : 25 = 2,56
================
oraz
I PB I*I PCI = I PAI 2
I PA I2 = 2,56*25 = 64
=================
11 maj 15:25
5-latek: A teraz Lili zajrzy do ksiazki i napisze z jakie twierdzenia skorzystal Janek
11 maj 15:29
Janek191:
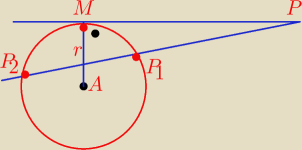
Tw. Jeżeli przez punkt leżący poza okręgiem poprowadzimy styczną do tego okręgu
w punkcie M i sieczną przecinającą ten okrąg w punktach P
1 i P
2 , to
I P P
1 I*I P P
2 I = I P M I
2 = I A P I
2 − r
2
==================================_
11 maj 15:33
Janek191:

Tw. Jeżeli przez punkt leżący poza okręgiem poprowadzimy styczną do tego okręgu
w punkcie M i sieczną przecinającą ten okrąg w punktach P
1 i P
2 , to
I P P
1 I*I P P
2 I = I P M I
2 = I A P I
2 − r
2
===================================
11 maj 15:33
5-latek: Janek ja wiem ze TY to znasz ale czy zna nasza kolezanka
11 maj 15:34
Janek191:
Ciekawe czy zdążyła zajrzeć do książki ?

11 maj 15:35
pigor: ..., korzystasz z tw. o stycznej lub siecznej i
tw. Pitagorasa
otóż, |AO|=|OC|=15, wtedy z ΔPAO prostokątnego :
|PA|
2=|PO|
2−|AO|
2 ⇒ |PA|
2=17
2−15
2=2*32=64 ⇒
|PA|= 8
a z tw. o stycznej i siecznej
|PA|2=|PB|*|PC| ⇒ 8
2=|PB|*25 ⇔
|PB|= 6425=2
1425=
2,56.

11 maj 15:43
Lili: Bardzo dziękuję za pomoc

i zajrzałam do książki, a to że niestety nie umiałam wykorzystać
tego w praktyce, to już inna sprawa

Jeszcze raz serdecznie dziękuję

11 maj 16:13
 Z punktu P poprowadzono styczną w punkcie A do okręgu o środku O oraz sieczną przecinającą
okrąg w punktach B i C (rysunek)
Wiedząc, że |PC|=25 ,|CO|=15, |OP|=17. Oblicz |PA|, |PB|
Bardzo proszę o pomoc, jakąkolwiek wskazówkę w jakim kierunku powinnam iść
Z punktu P poprowadzono styczną w punkcie A do okręgu o środku O oraz sieczną przecinającą
okrąg w punktach B i C (rysunek)
Wiedząc, że |PC|=25 ,|CO|=15, |OP|=17. Oblicz |PA|, |PB|
Bardzo proszę o pomoc, jakąkolwiek wskazówkę w jakim kierunku powinnam iść
 Tw. Jeżeli przez punkt leżący poza okręgiem poprowadzimy styczną do tego okręgu
w punkcie M i sieczną przecinającą ten okrąg w punktach P1 i P2 , to
I P P1 I*I P P2 I = I P M I2 = I A P I2 − r2
==================================_
Tw. Jeżeli przez punkt leżący poza okręgiem poprowadzimy styczną do tego okręgu
w punkcie M i sieczną przecinającą ten okrąg w punktach P1 i P2 , to
I P P1 I*I P P2 I = I P M I2 = I A P I2 − r2
==================================_
 Tw. Jeżeli przez punkt leżący poza okręgiem poprowadzimy styczną do tego okręgu
w punkcie M i sieczną przecinającą ten okrąg w punktach P1 i P2 , to
I P P1 I*I P P2 I = I P M I2 = I A P I2 − r2
===================================
Tw. Jeżeli przez punkt leżący poza okręgiem poprowadzimy styczną do tego okręgu
w punkcie M i sieczną przecinającą ten okrąg w punktach P1 i P2 , to
I P P1 I*I P P2 I = I P M I2 = I A P I2 − r2
===================================


 i zajrzałam do książki, a to że niestety nie umiałam wykorzystać
tego w praktyce, to już inna sprawa
i zajrzałam do książki, a to że niestety nie umiałam wykorzystać
tego w praktyce, to już inna sprawa Jeszcze raz serdecznie dziękuję
Jeszcze raz serdecznie dziękuję 