ciągi
łatka: Wyznacz ogólny wyraz ciągu (an), jeśli suma n początkowych jego wyrazów wyraża się wzorem
Sn= n2 − 29n / 4
11 maj 14:24
...:
| | n2−29n | | 29n | |
Sn= |
| czy Sn=n2− |
| |
| | 4 | | 4 | |
11 maj 14:38
5-latek: Otoz an= Sn−Sn−1
11 maj 14:44
łatka: Sn= (n2 − 29n) to całe w liczniku , podzielone przez 4
11 maj 19:07
5-latek: No to tearz zeby obliczyc S
n−1 wstawiamy w miejscr n do wzoru na S
n n−1i dostajemy
| | (n−1)2−29(n−1) | |
Sn−1= |
| i to liczymy wiec prosze to policzyc |
| | 4 | |
11 maj 19:13
daisy: czyli
n2−2n−1−29n−29/4
n2−31n−30/4
11 maj 19:18
5-latek: No to teraz odejnij Sn−Sn−1
11 maj 19:21
daisy: a tak bez zbędnych hejtów to skąd jest ten wzór an= sn − Sn−1
11 maj 19:46
zawodus: A czym jest Sn?
11 maj 19:47
daisy: sumą początkowych wyrazów ciągu
11 maj 19:48
zawodus: To teraz rozpisz sobie po kolei S1,S2,S3... i wyznacz an w zależności od tych sum.
11 maj 19:51
Eta:
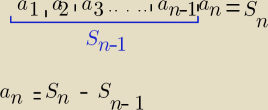
11 maj 19:51
Eta:
Oczywiście .....zamiast przecinków miały być +
11 maj 19:52