muszę znaleźć prostą prostopadłą do AB przechodzacą przez punkt P(5,2)
donut: Cześć, przy rozwiazywaniu zadania zaciąłem się na jednej, wydaje mi się, że bardzo prostej
rzeczy, ale nie mogę wyjść z zagwozdki.
Otóż mam prostą AB o równaniu kierunkowym y=2
Teraz muszę znaleźć prostą prostopadłą do AB przechodzacą przez punkt P(5,2)
Zatem prosta prostopadła to będzie x=5
Nie mogę tylko zrozumieć, dlaczego tak jest? Prosta prostopadła to taka, która ma odwrotny
wpsółczynnik kierunkowy. Zatem podstawiając do równania kierunkowego prostej y=ax+b wychodzi
mi tak czy tak, że y=2
2=5*0+b
2=b
zatem y=2
W jaki sposób jakoś pokazać, że prostą prostopadłą jest x=5?
11 maj 13:30
5-latek:
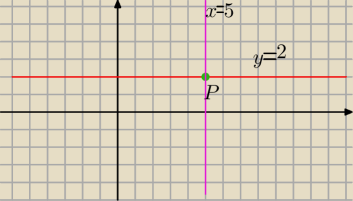
11 maj 13:34
donut: oczywiście wyobrazam sobie to na osi współrzędnych, ale czy w zadaniu wystarczy napisać, że
skoro
AB: y=5
symetralna przechodzi przez punkt P (5,2)
to równanie prostej symetralnej do AB to x=2 ?
11 maj 13:37
...:
... to "pobaw się" warunkami prostopadłości −

x=2 funkcją nie jest ... prawa dotyczące funkcji nie tutaj −

11 maj 14:02
pigor: ..., znaleźć prostą prostopadłą do prostej
y=2 przechodzącą przez punkt
P=(5,2)
−−−−−−−−−−−−−−−−−−−−−−−−
a to pytanie: w jaki sposób jakoś pokazać, że
prostą prostopadłą do y=2, jest x=5 ?
bardzo dobrze świadczy o Tobie; tak trzymaj...

−−−−−−−−−−−−−−−−−−−−−−
otóż, graficznie sprawa prosta, a analitycznie (rachunkowo) , to
postać kierunkową prostej y=ax+b zostaw dla profilu podstawowego,
a poczytaj o równaniu ogólnym prostej
Ax+By+C=0 i wynikającej
z niego równania prostej przez 1 punkt (*)
A(x−xo)+B(y−yo)=0,
gdzie [A,B] − wektor ⊥ do tej prostej ;
−−−−−−−−−−−−−−−
a więc łopatologicznie rzecz ujmując masz :
y=2 ⇔ 0x+1y−2=0 ⇒
[A,B]=[0,1] i
(xo,yo)=(5,2) , stąd i z (*) :
0(x−5)+2(y−2)= 0 ⇔ 0+2(y−2)= 0 ⇔ 2(y−2)=0 ⇔ y−2=0 ⇔
y=2 . ...

11 maj 14:34
...:
nie 0(x−5)+2(y−2)= 0 tylko ...
11 maj 14:52
PW: Cytat z 13:30: Prosta prostopadła to taka, która ma odwrotny
wpsółczynnik kierunkowy.
Jak zwykle kłania się dokładna znajomość treści twierdzeń (nie potocznej wersji, a dokładnej −
ze wszystkimi założeniami). Jak sobie wyobrażasz prostą prostopadłą do
y = 0•x + 2.
| | 1 | |
Miałaby mieć współczynnik kierunkowy a= |
| ? |
| | 0 | |
11 maj 17:45
5-latek: Bardzo sluszna uwaga
11 maj 17:48
pigor: ..., aaaaaaaa. kurcze, dzieki
...: ; przepraszam oczywiście
1...
a tak się ...

starałem i ...

poświęciłem

11 maj 18:06
donut: pigor −> z twojego wyjaśnienia dalej wychodzi na to, że y=2, ale skąd ma wyjść, że prosta
prostopadła to x=5?

PW −> tak, w takim razie prosta prostopadła do y=2 ma również współczynnik a=0, a co za tym
idzie jest to funkcja stała.
Tak czy tak, dziękuję Wam za wszystko!

11 maj 21:17
PW: O to idzie, że pojęcie współczynnika kierunkowego ma sens tylko dla prostych, które nie są
prostopadłe do osi OX. Prosta x=5 (prostopadła do osi OX) nie ma współczynnika
kierunkowego.
Mam tylko jedną radę na takie wątpliwości: książka, temat "współczynnik kierunkowy prostej"
i dokładnie przeczytać wszystkie założenia.
11 maj 21:42
donut: PW −> teraz wszystko rozumiem, w książce nie mogłem znaleźć żadnych informacji na ten temat,
nauczycielka tak leci, że pierwszy raz słyszę o tym, ze jeśli prosta jest równoległa do osi OY
(lub prostopadła do OX, jak kto woli) to nie można wtedy wyznaczyć równania prostej w postaci
kierunkowej, nie wyznacza sie wtedy współczynnika kierunkowego, ani nic z tych rzeczy. Winny
się tłumaczy, przyznaję swoje niedopatrzenia i pewną "głupotę" ale wielkie, wielkie dzięki za
to, że naświetliłeś mi sprawę jasno. Ogromny szacunek i ukłon z mojej strony!
11 maj 22:01
PW: 
Można jeszcze tak zapamiętać: współczynnik kierunkowy to
tangens kata nachylenia
prostej do osi OX. Tangens 90° nie istnieje (to wiemy z definicji tangensa), a więc nie można
mówić w tym wypadku o współczynniku kierunkowym.
11 maj 22:10
...:
Współczynnik kierunkowy dotyczy funkcji f(x)=ax+b
f(x)=2 jest funkcją stała ... a=0
x=5
funkcją nie jest 
11 maj 22:31

 x=2 funkcją nie jest ... prawa dotyczące funkcji nie tutaj −
x=2 funkcją nie jest ... prawa dotyczące funkcji nie tutaj −
 −−−−−−−−−−−−−−−−−−−−−−
otóż, graficznie sprawa prosta, a analitycznie (rachunkowo) , to
postać kierunkową prostej y=ax+b zostaw dla profilu podstawowego,
a poczytaj o równaniu ogólnym prostej Ax+By+C=0 i wynikającej
z niego równania prostej przez 1 punkt (*) A(x−xo)+B(y−yo)=0,
gdzie [A,B] − wektor ⊥ do tej prostej ;
−−−−−−−−−−−−−−−
a więc łopatologicznie rzecz ujmując masz :
y=2 ⇔ 0x+1y−2=0 ⇒ [A,B]=[0,1] i (xo,yo)=(5,2) , stąd i z (*) :
0(x−5)+2(y−2)= 0 ⇔ 0+2(y−2)= 0 ⇔ 2(y−2)=0 ⇔ y−2=0 ⇔ y=2 . ...
−−−−−−−−−−−−−−−−−−−−−−
otóż, graficznie sprawa prosta, a analitycznie (rachunkowo) , to
postać kierunkową prostej y=ax+b zostaw dla profilu podstawowego,
a poczytaj o równaniu ogólnym prostej Ax+By+C=0 i wynikającej
z niego równania prostej przez 1 punkt (*) A(x−xo)+B(y−yo)=0,
gdzie [A,B] − wektor ⊥ do tej prostej ;
−−−−−−−−−−−−−−−
a więc łopatologicznie rzecz ujmując masz :
y=2 ⇔ 0x+1y−2=0 ⇒ [A,B]=[0,1] i (xo,yo)=(5,2) , stąd i z (*) :
0(x−5)+2(y−2)= 0 ⇔ 0+2(y−2)= 0 ⇔ 2(y−2)=0 ⇔ y−2=0 ⇔ y=2 . ... 
 starałem i ...
starałem i ...  poświęciłem
poświęciłem 
 PW −> tak, w takim razie prosta prostopadła do y=2 ma również współczynnik a=0, a co za tym
idzie jest to funkcja stała.
Tak czy tak, dziękuję Wam za wszystko!
PW −> tak, w takim razie prosta prostopadła do y=2 ma również współczynnik a=0, a co za tym
idzie jest to funkcja stała.
Tak czy tak, dziękuję Wam za wszystko! 
 Można jeszcze tak zapamiętać: współczynnik kierunkowy to tangens kata nachylenia
prostej do osi OX. Tangens 90° nie istnieje (to wiemy z definicji tangensa), a więc nie można
mówić w tym wypadku o współczynniku kierunkowym.
Można jeszcze tak zapamiętać: współczynnik kierunkowy to tangens kata nachylenia
prostej do osi OX. Tangens 90° nie istnieje (to wiemy z definicji tangensa), a więc nie można
mówić w tym wypadku o współczynniku kierunkowym.
