Geometria analityczna grucha: Wyznacz współrzędne środka okręgu opisanego na trójkącie ABC oraz oblicz ptomień tego okręgu, gdy A(−2,2) B(4,−4) C(12,2) Obliczyłem symetralną odcinka AC −> x=5 Następnie obliczyłem symetralną odcinka AB, wyszło, iż x=y Zatem środek okręgu wg mnie to O(5,5) Jednak gdy obliczam promień czyli R=|OA|=|OB|=|AC| wychodzą mi inne wyniki z kazdego odcinka, a przecież promień musi być ten sam.. Czy kto mógłby mi pomóc

5-latek: A co to jest wedlug Ciebie symetralna ?

grucha: prosta przecinająca bok trójkąta na dwie równe części, tak najprościej mówiąc

grucha: oczywiście pod katem prostym, prosta prostopadła

5-latek: Dobrze . WieC srodek S odcinka AC x_AC= 5 i y_AC=2 (wzor na srodek odcinka czyli S_AC(5,2) i teraqz napisz rownanie symetralnej prostej AC i przechodzacej przez punkt S(5,2) tak samo Policz wsporzedne srodka odcinka AB i napisz rownanie symetralnej AB Potem wylicz punkt przeciecia sie symetralnych i dostaniesz wspolrzedne srodka okregu teraz np dlugosc AS to promiern

grucha: w takim razie rownanie symetralnej prostej AC przechodzacej przez AC: 5=2a+b Współrzędne środka odcinka AB to S(1,−1) zatem symetralna odcinka AB to −1=a+b

Bogdan: Inny sposób i chyba wymagający mniej obliczeń. okrąg: x² + y² + ax + by + c = 0,

	a		b
środek S = (x0, y0), x0 = −		, y0 = −
	2		2

długość promienia r = √x₀² + y₀² − c Układ równań: 1) 4 + 4 − 2a + 2b + c = 0 ⇒ c = 2a − 2b − 8 2) 16 + 16 + 4a − 4b + c = 0 ⇒ 32 + 4a − 4b + 2a − 2b − 8 = 0 ⇒ 6a − 6b = −24 3) 144 + 4 + 12a + 2b + c = 0 ⇒ 148 + 12a + 2b + 2a − 2b − 8 = 0 ⇒ 14a = −140 ⇒ a = −10 2) a − b = −4 ⇒ −10 − b = −4 ⇒ b = −6 1) c = −20 + 12 − 8 = −16

	−10		−6
Środek S = (−		, −		) = (5, 3), długość promienia r = √25 + 9 + 16 = 5√2
	2		2

grucha: niestety takich wzorów nie mieliśmy nawet na lekcji, dlatego to nie przejdzie Ale wielkie Dzięki Bogdan!

Bogdan: Nie ma tu nic nadzwyczajnego, są to proste przekształcenia, każdy może je sobie sam wykonać. (x − x₀)² + (y − y₀)² = r² x² − 2x₀x + x₀² + y² − 2y₀y + y₀² − r² = 0 −2x₀ = a, −2y₀ = b, x₀² + y₀² − r² = c

	−a		−b
x0 =		, y0 =		, r = √x02 + y02 − c
	2		2

x² + y² + ax + by + c = 0

Bogdan: Można także rozwiązać taki układ równań: (x + 2)² + (y − 2)² = r² (x − 4)² + (y + 4)² = r² (x − 12)² + (y − 2)² = r²

grucha: A czy potrafisz to zrobić korzystając z wyliczenia symetralnych odcinków? Kompletnie nie mam pojęcia jak się za to zabrać, dwa pierwsze przykłady z zadania ładnie mi poszły, a teraz robiąc wszystko analogicznie nie wychodzi nic..

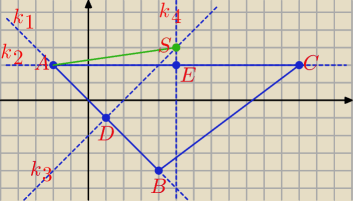
Bogdan: D = (1, −1), E = (5, 2), Prosta AB: k₁: y = a₁x + b₁, a₁ = −1, prosta k₃: y = a₃x + b₃ i D∊k₃ i k₃⊥k₁ ⇒ y = (x − 1) − 1 ⇒ y = x − 2 Prosta AC: k₂: y = 2, prosta k₄: E∊k₄ i k₄⊥k₂ ⇒ k₄: x = 5 S = k₂∩k₄ ⇒ x = 5 i y = 5 − 2 = 3, S = (5, 3) Długość promienia r = |AS| = ...

grucha: Rzeczywiście, gdy z tych współrzędnych wylicze promień to wszystko ładnie wychodzi. Następny przykład zrobiłem bez problemu, dziękuję, jesteś WIELKI!