xyz prawd
letsgo: Jadę dalej z tym prawdopodobieństwem.
Rzucamy dwa razy sześcienną kostką, której jedna ściana ma jedno oczko, dwie ściany mają po dwa
oczka i trzy ściany mają po trzy oczka. Oblicz prawdopodobieństwo zdarzenia: A − liczby oczek
otrzymane w obu rzutach różnią się o 1
10 maj 22:57
letsgo: Wróć, ja już chyba te zadanie robiłem.
10 maj 22:58
Mario: Napisz,prosze,rozwiazanie

10 maj 23:02
letsgo:

|Ω| = 36
|A|=16
10 maj 23:02
letsgo: sorki, poprzesuwało mi się wszystko w tabelce, zrobię ją jeszcze raz
10 maj 23:03
letsgo:
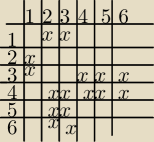
Proszę bardzo, jak chcesz porobić zadanka z tego działu, to mam ich do zrobienia około 180,
przy tym 50 już za sobą. Napisz, to mogę wysłać.
10 maj 23:07
PW: Ω składa się z 3•3 = 9 zdarzeń elementarnych, które niestety nie są jednakowo prawdopodobne
(nie działa twierdzenie zwane klasyczną definicją prawdopodobieństwa).
Wskazówka: twierdzenie o prawdopodobieństwie w przestrzeni produktowej Ω×Ω dla pary doświadczeń
przebiegającyh niezależnie od siebie).
10 maj 23:18
letsgo: Czyli mam źle?
10 maj 23:19
letsgo: Aaaa, o kurde , tam nie powinno być 1,2,3,4,5,6 tylko 1,2,2,3,3,3
To miałeś na myśli? Przerysowałem dla kolegi Mario, a nie patrzyłem na treść.
10 maj 23:20
Mario: nie bardzo tabelke zrozumielem((
Jak mi wyslac mozesz?
10 maj 23:27
letsgo: Na maila bodajże
10 maj 23:29
letsgo: Mario, czego nie rozumiesz? Zerknij,
powiedzmy 4 wiersz i 5 kolumna, różnica między dwiema kostkami jest jeden
10 maj 23:30
letsgo: Niestety prawdopodobieństwo to taki dział, że zrozumienie problemu jest ważniejsze niż jego
rozwiązanie

10 maj 23:31
PW: (1) P(ω
i,ω
j) = P
1(ω
i)•P
2(w
j), i,j∊{1,2,3).
W tym zadaniu
P
2(ω
k)=P
1(ω
k) dla wszystkich k∊{1,2,3),
a więc (1) upraszcza się do
(2) P(ω
i,ω
j) = P
1(ω
i)•P
1(w
j), i,j∊{1,2,3).
Prawdopodobieństwa P
1(1), P
1(2) i P
1(3) obliczamy w pamięci rozwiązując "malutkie zadanie na
klasyczną definicję prawdopodobieństwa":
| | 1 | | 2 | | 3 | |
P1(1) = |
| , P1(2) = |
| , P1(3) = |
| . |
| | 6 | | 6 | | 6 | |
Ω = {(1,1), (1,2), (2,1), (2,2), (1,3), (3,1), (2,3), (3,2), (3,3)} (to tylko dla porządku, nie
wykorzystujemy tego do obliczeń).
A = {(1,2), (2,1) ....}
i tak po prostu po wypisaniu całego A policzyć każde prawdopodobieństwo zdarzenia elementarnego
wzorem (2).
10 maj 23:33
letsgo: Ciekawe. Pomyślę i postaram się to rozwiązać.
bardzo dziękuję za twoją pomoc
10 maj 23:37
Mario: mariush
m@bigmir.net

11 maj 00:00
letsgo: mariushm tak?
11 maj 00:06
Mario: miedzy imieniem i literka minus na dole _
11 maj 00:07
letsgo: napisz jeszcze raz
11 maj 00:07
letsgo: to po co te m dałeś?
11 maj 00:08
letsgo: aha, już wiem, wysyłam
11 maj 00:13
Hugo:
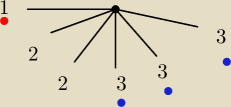
Ω= 36
bo
jedną kostką można na 6 sposobów i potem drugą też =>6*6
A
Wypisujemy mozliwości
1 i 2 lub 2 i 1 lub 3 i 2 lub 2 i 3(różnica 1 )
1−> 2
1−>2'
2−>3
2−>3'
2−>3''
2'−3
2'−3'
2'−3''
(x2 w drugą strone)
2−1
2−1
3−2....
Moc A = 8*2=16
P(A)=16/36=4/9
//tak wdł mnie na logike ale PW jest mądrzejszy patrz do niego

11 maj 00:28
letsgo: dzięki za pomoc, ale jeszcze rozwiąże sposobem PW, całą nockę jeszcze mam
11 maj 00:32

 |Ω| = 36
|A|=16
|Ω| = 36
|A|=16
 Proszę bardzo, jak chcesz porobić zadanka z tego działu, to mam ich do zrobienia około 180,
przy tym 50 już za sobą. Napisz, to mogę wysłać.
Proszę bardzo, jak chcesz porobić zadanka z tego działu, to mam ich do zrobienia około 180,
przy tym 50 już za sobą. Napisz, to mogę wysłać.


 Ω= 36
bo
jedną kostką można na 6 sposobów i potem drugą też =>6*6
A
Wypisujemy mozliwości
1 i 2 lub 2 i 1 lub 3 i 2 lub 2 i 3(różnica 1 )
1−> 2
1−>2'
2−>3
2−>3'
2−>3''
2'−3
2'−3'
2'−3''
(x2 w drugą strone)
2−1
2−1
3−2....
Moc A = 8*2=16
P(A)=16/36=4/9
//tak wdł mnie na logike ale PW jest mądrzejszy patrz do niego
Ω= 36
bo
jedną kostką można na 6 sposobów i potem drugą też =>6*6
A
Wypisujemy mozliwości
1 i 2 lub 2 i 1 lub 3 i 2 lub 2 i 3(różnica 1 )
1−> 2
1−>2'
2−>3
2−>3'
2−>3''
2'−3
2'−3'
2'−3''
(x2 w drugą strone)
2−1
2−1
3−2....
Moc A = 8*2=16
P(A)=16/36=4/9
//tak wdł mnie na logike ale PW jest mądrzejszy patrz do niego 