Wykaż, że funkcja jest malejąca. Radek: Witam Mam pytanie jak wykazać, że funkcja −5x²+4 jest malejąca w przedziale 0 do nieskończoności ? Dziękuje za pomoc

5-latek: Z definicji . Dla kazdego x₁<x₂ f(x₁)>f(x₂)

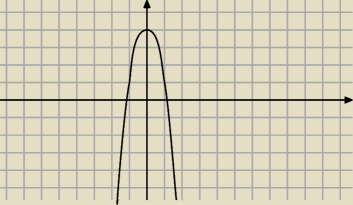
Hajtowy: Gdzieś tam sobie leci

Radek: Hmyy w sumie ta definicja mi nic nie mówi jak ją wykorzystać ?

PW: Tak jak pisze 5−latek, wziąć dwa dowolne elementy z podanego zbioru: x₁ < x₂ (niestety teoretyczne, nie konkretne) i badać różnicę f(x₁) − f(x₂) − jeżeli będzie dodatnia − to znaczy że f(x₁)>f(x₂), czyli funkcja jest malejąca.

Radek: −5_x1²+4+5_x2²−4 dobrze ?

Mila: x₁,x₂∊(0,∞) (są dodatnie) badamy dla x₁<x₂ znak różnicy f(x₁)−f(x₂) dla x₁<x₂ mamy x₁−x₂<0 f(x₁)−f(x₂)=−5x₁²+4−(−5x₂+4)= =−5x₁²+4+5x₂²−4=5*(x₂²−x₁²)=5*(x₂+x₁)*(x₂−x₁)>0⇔ dla x₁<x₂ mamy f(x₁)>f(x₂)⇔f(x) jest malejąca dla x∊(0,∞)

pie: Można jeszcze pochodną policzyć.

Mila: Na poziomie studiów tak.

pie: Nowa podstawa, druga klasa.