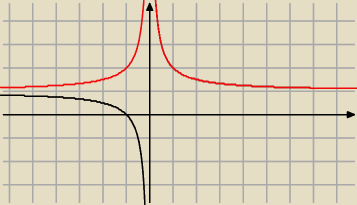
Jak narysować te wykresy ? Do każdego podpunktu jeden wykres. Ola: We wspólnym układzie współrzędnych wykonaj wykresy funkcji: a) f(x)= x−3 i g(x)= |x−3| b) f(x)= 1/x +1 i g(x)= 1/|x| +1 c) f(x)=√x+4 i g(x0= √|x| + 4 d) f(x)=x² −1 i g(x)= |x² −1 |

PW: Nie narysuję, bo nie opanowałem tej sztuki. Mogę napisać. Te ćwiczonka mają Ci uzmysłowić różnicę między wykresami funkcji f(x) i g(x) =|f(x)| (punkty a) i d) oraz między f(x) i f(|x|) (punkty b) i c). W pierwszym wypadku ta część wykresu, która leży nad osią OX zostaje bez zmian, a leżącą pod osią należy przekształcić przez symetrię względem osi OX (jak to mówią potocznie "odbić do góry"). b) Drugi rodzaj zmiany polega na tym, że dla x>0 wykres g(x) jest taki sam jak f(x) − tu nic nie zmieniamy, bo |x| = x, a więc i g(x) = f(x)), natomiast część wykresu leżącą nad (pod) ujemną półosią pomijamy, a zastępujemy ją kawałkiem wykresu leżącym po przeciwnej stronie osi OY − przekształconym symetrycznie względem tej osi. c) jest najtrudniejsze z tej przyczyny, że dziedziną f jest [−4,∞), a dziedziną g jest cała oś R. Rysujemy g(x) dla x≥0 a następnie dodajemy do tego drugi kawałek wykresu g leżący nad ujemną półosią − symetryczny do tego poprzedniego względem osi OY.

Insane: co do podpunktu b, to tutaj zmienia się i to sporo. Cała funkcja "kopiuje się" z prawej strony na lewą. Tak mi się przynajmniej wydaje, z zadań z roszerzenia.

5-latek: Witam PW Wlasnie sie nauczylem . Klikasz na rysuje i pojawi sie siatka Nastepnie klikasz na okienko z ukladem wspolrzednych i potem na sitake kilikasz raz i rozciagasz myszka zeby dostac wieksze kratki . W okienko gdzie piszse y= wpisujesz wzor funnkcji i klikasz na okienko z wykresem . Mozesz rowniez zmienic sobie kolor na inny niz czarny

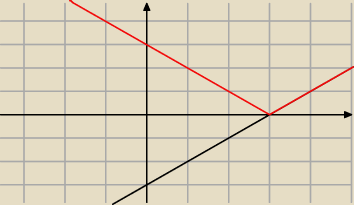
jakubs: Czerwony to |x−3| czarny x−3

jakubs:

	1
Czarny		+1
	x

	1
Czerwony		+1
	|x|

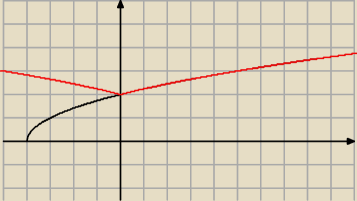
jakubs: Czarny (x+4)⁽1/2) Czerwony (|x|+4)⁽1/2)

jakubs: Czarny √(x+4) Czerwony √(|x|+4)

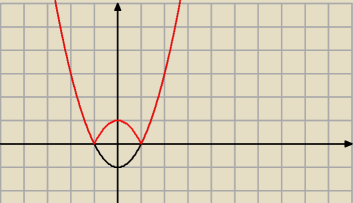
jakubs: Czarny x²−1 Czerwony |x²−1|

jakubs: Na niektórych kiepsko widać, bo się pokrywają, ale jak mają być na wspólnym układzie to są

PW: Dziękuję, koledzy. Wspólnymi siłami praca domowa odrobiona

Ola: Dziękuje wam bardzo!

5-latek: To dobrze z e dziekujesz ale czy to rozumiesz ?

zawodus: Ja rozumiem Teraz zadamy Oli pracę domową i sprawdzimy