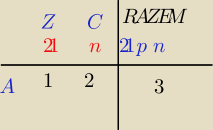prawdpo
letsgo: W urnie jest 21 kul zielonych. Ile kul czerwonych trzeba dorzucić, aby prawdopodobieństwo
wylosowania kuli czerwonej było równe 0,3?
x− czerwone
tak?
10 maj 20:01
mat: tak
10 maj 20:11
JL: Gratuluję....
10 maj 20:14
letsgo:

dzięki mat
no to mam drugie pytanie, nie będę nowego wątku zakładał
Rzucamy dwoma kostkami do gry. Oblicz prawd tego, że na każdej kostce wypadły co najwyżej 3
oczka.
|omega| = 36
|A| = 9
P(A) = 1/4
10 maj 20:16
Bogdan:

| | | | 3 | | n | | 3 | |
P(A) = |
| = |
| ⇒ |
| = |
| ⇒ n = 9 |
| | | | 10 | | 21 + n | | 10 | |
10 maj 20:25
letsgo: Bogdan wytłumacz mi czym są te wartości 0 i 1 w podzbiorze A?
Widzę, że ten twój sposób jest uniwersalny.
10 maj 20:30
letsgo: mam na myśli ten rysunek
10 maj 20:30
Bogdan:
zero wylosowanych kul zielonych, jedna wylosowana kula czerwona, razem wylosowano
jedną kulę ze zbioru n+21 kul

10 maj 20:33
letsgo: Wszystko mi się teraz zgadza. Czyli tak: jeśli prawdopodobieństwo wylosowania dwóch kuł byłoby
równe 0,3 , to zamiast 1 wpisuję 2 i w razem 2 również, tak?
10 maj 20:36
letsgo: A później to już działanie na symbolach newtona,
10 maj 20:37
letsgo: Przekształciłem moje zadanie wyżej na nowe
W urnie jest 21 kul zielonych. Ile kul czerwonych trzeba dorzucić, aby prawdopodobieństwo
wylosowania dwóch kul czerwonych i jednej kuli zielonej było równe 0,3?
10 maj 20:40
letsgo:
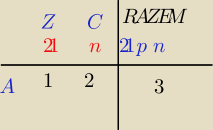
10 maj 20:43
10 maj 20:44
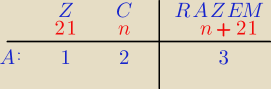
Bogdan:
10 maj 20:45
10 maj 20:45
10 maj 20:47
letsgo: Dzięki! Dla mnie jesteś geniuszem. Właśnie tak samo mi wyszło jak tobie. Dzięki, bo gdyby nie
ty, to nie potrafiłbym rozwiązywać tych zadań w ten sposób. Jesteś dla mnie jak nauczyciel.
10 maj 20:47
letsgo: Właśnie zerknąłem do przykładów i źle zapisywałem, bo ja pisałem przy pomocy wzoru U { } { }
, a tutaj należy N { } { }
10 maj 20:48
Bogdan:

10 maj 20:48
letsgo: Bogdan, a wiesz jak zobrazować moje drugie zadanie w ten sposób, czy raczej w postaci tabelki
będzie lepiej?
Rzucamy dwoma kostkami do gry. Oblicz prawd tego, że na każdej kostce wypadły co najwyżej 3
oczka.
10 maj 20:50
Bogdan:
|Ω| = 6
2 = 36, 6 liczb na dwóch miejscach,
|A| = 3
2 = 9, 3 liczby (jedynka, dwójka, trójka) na dwóch miejscach,
10 maj 20:53
letsgo: Czyli miałem dobrze (10 maja 20:16). Bardzo dziękuję!
10 maj 20:55
 dzięki mat
no to mam drugie pytanie, nie będę nowego wątku zakładał
Rzucamy dwoma kostkami do gry. Oblicz prawd tego, że na każdej kostce wypadły co najwyżej 3
oczka.
|omega| = 36
|A| = 9
P(A) = 1/4
dzięki mat
no to mam drugie pytanie, nie będę nowego wątku zakładał
Rzucamy dwoma kostkami do gry. Oblicz prawd tego, że na każdej kostce wypadły co najwyżej 3
oczka.
|omega| = 36
|A| = 9
P(A) = 1/4