objętość kuli alfa i omega: Obliczyć objętość kuli o promieniu R za pomocą całki podwójnej. Proszę o pomoc

MQ: Objętość, to chyba całki potrójnej. dV=r²sinθdrdθdφ V=∫∫∫r²sinθdrdθdφ wgranicach: r od 0 do R θ od −π do π φ od 0 do 2π

alfa i omega: No właśnie w zadaniu jest nadmienione że za pomocą całki podwójnej

MQ: No to chyba, że będziemy całkować po stożkach o wierzchołku w środku kuli i podstawie dS.

	1
Objętość takiego elementu to		RdS, a dS =R2sinθdθdφ
	3

i wtedy całkujemy po powierzchni kuli:

	1		1		1
V=∫∫		RdS=∫∫		R*R2sinθdθdφ=		R3∫∫sinθdθdφ
	3		3		3

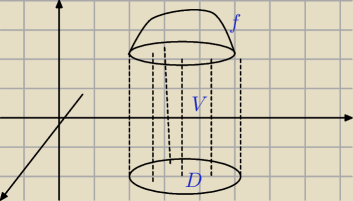
Vizer: Czyli objętość to : ∬_D f(x,y) dxdy ? Dawno miałem całki, ale wydaje mi się, że nie trzeba kombinować z jakimiś stożkami

alfa i omega: udało się, dzięki MQ i Vizer za pomoc