zadanie prawdpodobieńśtwo urny
letsgo:
Witam, mam tutaj dość skomplikowane zadanie z prawdopodobieństwa. To mój pierwszy kontakt z tym
działem. Mam takie zadanie:
W Urnie znajduje się 6 kul białych i 4 kule czarne. Z urny losujemy dwie kule. Oblicz
prawdopodobieństwo tego, że wylosowano kule różnych kolorów.
Do poniedziałku muszę ten dział opanować do perfekcji.
Chcę te zadanie rozwiązać na dwa sposoby
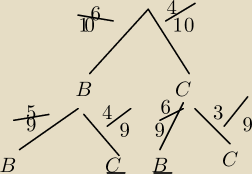
I − drzewkami (rysunek niżej)
II − tabelką
Obliczając prawdopodobieństwo przy pomocy drzewka mnożę
49 oraz
69 , tak?
P(A) =
49 *
69 =
49
Mylę się czy nie?
−−−−−−−−−−−−−
Przejdźmy do drugiego sposoby. Chcę te zadanie rozwiązać rysując tabelkę, ale nie bardzo wiem
jak ona ma wyglądać. Mój nieudaczny rysunek tabelki poniżej. Proszę sprawdzić i mnie poprawić.
10 maj 14:26
letsgo:
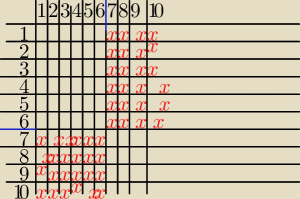
I teraz liczę prawdopodobieństwo:
|Ω|= 40
P(A) =
1040 =
14
No ale, wyniki się różni z tym co wyżej, dlaczego?
10 maj 14:32
hehe: A=6*4=24
P(A)=24/45
10 maj 14:34
letsgo: nie rozumiem
10 maj 14:37
letsgo: Dlaczego podzbiór A 6*4?
10 maj 14:39
10 maj 14:42
10 maj 14:43
letsgo: Jakubs, a te drzewko co zaprojektowałem jest dobre? Tabelka również?
10 maj 14:44
jakubs: Drzewko dobrze. Tabelki nie sprawdzałem.
10 maj 14:44
letsgo: Ja tego działu nie ogarniam, nigdy nie miałem z nim do czynienia, jakoś tak wyszło. Nawet
ciężko o porządne materiały do przerobienia z tego działu.
10 maj 14:44
letsgo: @jakubs
Ale tak na chłopski matematyczny rozum, jak sądzisz?
10 maj 14:45
Bogdan:

B − kula biała, C − kula czarna,
A − zdarzenie polegające na wylosowaniu dwóch kul różnych kolorów
| | | | 6 * 4 | | 24 | | 8 | |
P(A) = |
| = |
| = |
| = |
| |
| | | | | | 45 | | 15 | |
10 maj 14:46
jakubs: Ja nie mam matematycznego rozumu hehe
Nie rozkminiam tego pomysłu z tabelka, więc się nie wypowiem. Drzewko masz dobrze, ale coś źle
obliczyłeś. Zerknij na linka, który podrzuciłem i zobacz jak się oblicza prawdopodobieństwo z
drzewka .
10 maj 14:47
letsgo: Bogdan, bardzo dziękuję. Mam jeszcze pytanie do sposobu zapisu.
W liczniku napisałeś 6/1 ale bez kreski ułamkowej. Co to jest za zapis? Mógłbyś podać mi
odnośnik do odpowiedniej podstrony na matematyka.pisz.pl?
10 maj 14:48
Bogdan:
| | n * (n−1) * (n−2) * ... * (n−k+1) | |
= |
| |
| | 1 * 2 * 3 * ... * k | |
| | | | n! | |
a także | = |
| |
| | | k1 * (n − k)! | |
| | | | 7! | | 4! * 5 * 6 * 7 | | 5*6*7 | |
np.: | = |
| = |
| = |
| = ... |
| | | 3! * (7 − 3)! | | 1 * 2 * 3 * 4! | | 1*2*3 | |
Warto pamiętać:
10 maj 14:56
10 maj 14:57
letsgo: @jakubs dzięki
Liczę prawdpodobieńśtwo z drzewka 610 * 49 + 410 * 69 = 4890
10 maj 14:57
letsgo: @Bogdan
Bardzo dziękuję, staram się w dużej mierze samemu przygotowywać do maturki. Akurat takiego
zapisu nie znałem, dzięki!
10 maj 14:59
Bogdan:
Przykłady zastosowania symbolu Newtona
Dany jest zbiór n−elementowy, np zbiór liczb od 1 do 49. Wybieramy z tego zbioru
| | | |
6 dowolnych liczb. Możemy to wykonać na | sposobów. |
| | |
| | | |
Jest 10 drużyn piłkarskich, każda gra z każdą jeden mecz. Odbędzie się | spotkań, |
| | |
w każdym spotkaniu biorą udział dwie drużyny.
Wzór skróconego mnożenia:
| | | | | | | | | | | |
(a + b)4 = | a4b0+ | a3b1+ | a2b2+ | ab3+ | a0b4 = |
| | | | | | |
= a
4 + 4a
3b + 6a
2b
2 + 4ab
3 + b
4
10 maj 15:14
letsgo: O, bardzo dziękuję. Mogę wręcz powiedzieć, że to moment przełomowy w mojej nauce. Dzięki za
klarownie objaśnienie. To są dla mnie świeże wiadomości, będę z tego korzystał na
sprawdzianie.
10 maj 15:20
zawodus: letsgo jesteś na podstawie mam rozumieć? Bo na rozszerzenie to raczej do klasy nie wpuszczają
bez znajomości symbolu Newtona

10 maj 15:22
letsgo: Jestem w klasie trzeciej, skończyliśmy wszystkie działy, ale prawdopodobieństwo nauczyciel
zostawił na koniec. Ogólnie nie mam problemów, raczej jestem samoukiem, a w szkole problemów
nie mam.
10 maj 15:24
zawodus: Dobra nie dostałem odpowiedzi na pytanie o poziom

10 maj 15:25
letsgo: Rozszerzony rzecz jasna
10 maj 15:26
PW: Cytat: "Do poniedziałku muszę ten dział opanować do perfekcji."
Z wrodzoną zjadliwością zapytam:
− Do poniedziałku, ale w którym roku − 2018?
Dobrze, że podchodzisz optymistycznie, ale muszę Cię rozczarować. Są w tym dziale niewinne
pytania, nad którymi można myśleć tygodniami.
10 maj 15:45
letsgo: Dobra, ale z waszej strony jest to niegrzeczne. Ja się tu edukuje, mam do zrobienia n zadań i
tyle. To nie twój problem PW, jak ja go ogarnę. Pytam, jestem chętny do nauki, ale taki
komentarz jak twój jest zbędny w tym temacie.
10 maj 15:54
52: PW po prostu bardzo zwraca uwagę na słowo i określenie do
perfekcji jest mało realne

I to wszystko nie ma co się od razu zrażać. Rób swoje

10 maj 15:58
letsgo: Na przyszłość będę bacznie zwracał uwagę jakich słów używam. Dla mnie jest to przesadna
hiperpoprawność.To poziom liceum i tyle.
10 maj 16:00
PW: Nie lubię nadmiernych optymistów, żeby nie powiedzieć gorzej. Trochę pokory by się przydało −
realnej oceny własnych możliwości. Stanąłeś nad brzegiem jeziora, drugiego brzegu nie widać, a
Ty krzyczysz:
− W godzinę przepłynę.
Rzeczywiście komentarze są zbędne, ale sam zacząłeś od głupiej przechwałki. Trzeba było
poprzestać na treści zadania.
Pozdrawiam Cię, miałem zamiar Ci pomagać, ale skoro to nie mój problem ...
10 maj 16:08
zawodus: PW ostatnio widzę co raz więcej osób na forum z takim podejściem.
Potem jak im się nie uda, to zrzucają winę na wszystko tylko nie na siebie.
10 maj 16:14
letsgo: To nie ten poziom dyskusji. Nie jestem przesadnym optymistą. Do perfekcji nie oznacza, że mam
potrafić rozwiązać każdy problem. Czy tak ciężko pouczyć się do egzaminu? Bo do poniedziałku,
to powinno mi się udać. My chyba na innych falach odbieramy. Niczym się nie chwalę.
10 maj 16:19
 Witam, mam tutaj dość skomplikowane zadanie z prawdopodobieństwa. To mój pierwszy kontakt z tym
działem. Mam takie zadanie:
W Urnie znajduje się 6 kul białych i 4 kule czarne. Z urny losujemy dwie kule. Oblicz
prawdopodobieństwo tego, że wylosowano kule różnych kolorów.
Do poniedziałku muszę ten dział opanować do perfekcji.
Chcę te zadanie rozwiązać na dwa sposoby
I − drzewkami (rysunek niżej)
II − tabelką
Obliczając prawdopodobieństwo przy pomocy drzewka mnożę 49 oraz 69 , tak?
P(A) = 49 * 69 = 49
Mylę się czy nie?
−−−−−−−−−−−−−
Przejdźmy do drugiego sposoby. Chcę te zadanie rozwiązać rysując tabelkę, ale nie bardzo wiem
jak ona ma wyglądać. Mój nieudaczny rysunek tabelki poniżej. Proszę sprawdzić i mnie poprawić.
Witam, mam tutaj dość skomplikowane zadanie z prawdopodobieństwa. To mój pierwszy kontakt z tym
działem. Mam takie zadanie:
W Urnie znajduje się 6 kul białych i 4 kule czarne. Z urny losujemy dwie kule. Oblicz
prawdopodobieństwo tego, że wylosowano kule różnych kolorów.
Do poniedziałku muszę ten dział opanować do perfekcji.
Chcę te zadanie rozwiązać na dwa sposoby
I − drzewkami (rysunek niżej)
II − tabelką
Obliczając prawdopodobieństwo przy pomocy drzewka mnożę 49 oraz 69 , tak?
P(A) = 49 * 69 = 49
Mylę się czy nie?
−−−−−−−−−−−−−
Przejdźmy do drugiego sposoby. Chcę te zadanie rozwiązać rysując tabelkę, ale nie bardzo wiem
jak ona ma wyglądać. Mój nieudaczny rysunek tabelki poniżej. Proszę sprawdzić i mnie poprawić.
 I teraz liczę prawdopodobieństwo:
|Ω|= 40
P(A) = 1040 = 14
No ale, wyniki się różni z tym co wyżej, dlaczego?
I teraz liczę prawdopodobieństwo:
|Ω|= 40
P(A) = 1040 = 14
No ale, wyniki się różni z tym co wyżej, dlaczego?
 B − kula biała, C − kula czarna,
A − zdarzenie polegające na wylosowaniu dwóch kul różnych kolorów
B − kula biała, C − kula czarna,
A − zdarzenie polegające na wylosowaniu dwóch kul różnych kolorów


 I to wszystko nie ma co się od razu zrażać. Rób swoje
I to wszystko nie ma co się od razu zrażać. Rób swoje 