Oblicz pole trójkąta ABC nieznany : Przez punkt D leżący na boku AB trójkąta ABC poprowadzono dwie proste. Pierwsza z nich, równoległa do boku BC, przecięła bok AC w punkcie F, a druga równoległa do boku AC, przecięła bok BC w punkcie E. Oblicz pole trójkąta ABC, wiedząc, że pola trójkątów ADF i DBE wznoszą odpowiednio 3a i a.

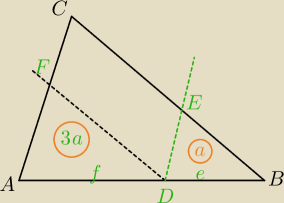
Mila: FD||BC DE||AC⇔ ΔADF∼ΔABC ΔADF∼ΔDBE Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa

PΔADF		3a
	=		=3=k2
PΔDBE		a

k=√3⇔ f=√3 e

	f+e		√3e+e
ΔABC∼ΔADF w skali k1=		=
	f		√3e

	√3+1
k1=
	√3

	√3+1
PΔABC=k12*PΔADF= (		)2*3a
	√3

P_ΔABC=(4+2√3)a =================

pigor: ..., widzę to tak: niech P_ΔDEC=P_ΔDFC=x, to P_ΔABC=4a+2x=?, a z tw. Talesa i i stosunku pól par trójkątów o jednakowych wysokościach :

	|BD|		|BE|		x+a		a
mam np.:		=		⇒		=		⇔
	|DA|		|EC|		x+3a		x

⇔ x(x+a)= a(x+3a) ⇔ x²= 3a² ⇒ x=a√3, zatem P_ΔABC= 4a+2a√3= 2a(2+√3) − szukane pole . ... −−−−−−−−−−−−−−−−−−−−−−−

nieznany : Dzięki bardzo za pomoc

Mila: