Okrąg wpisany i opisany - trójkat.
pie: Punkt S jest środkiem okręgu wpisanego w trójkąt ABC. Prosta przechodząca przez punkt Ci S
przecina okrąg opisany na trójkącie ABC w punkcie D. Wykaż, ze trójkąt BDS jest równoramienny.
Leżę z planimetrii.

8 maj 21:56
Nieuchwytny: Zrób rysunek.
8 maj 21:59
Donbi:
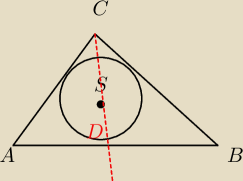
To może ja też zrobię bo średnio mi wychodzi planimetria

8 maj 22:07
aaaa:(:
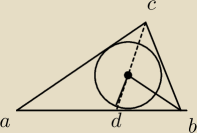
8 maj 22:09
Donbi:
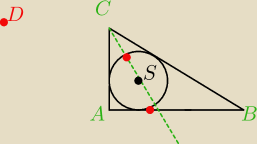
Dobrze? Bo nie za bardzo wiedziałem gdzie ten D dać u góry czy na dole

bo w sumie może być też tak:
8 maj 22:10
aaaa:(: też czekam na kogoś bo jestem ciekawy co i jak w tym zadanku

8 maj 22:13
pie:
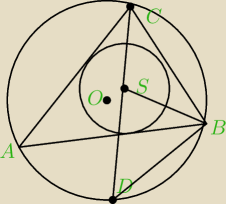
Jeśli już rysunek, to raczej tak.
8 maj 22:14
Donbi: CS nie będzie czasem dwusieczną?
8 maj 22:15
Donbi: ahh nie doczytałem tamtego, ale nadal pytam czy CS nie będzie dwusieczną?
8 maj 22:16
pie: Jeśli przechodzi przez środek okręgu wpisanego, to musi być.

8 maj 22:16
Donbi: Nie wiem co dalej

mała podpowiedź?
8 maj 22:19
Donbi:

CBX=β
BAC=γ
i dalej mam już problemy

8 maj 22:33
pie: Sam nie wiem.

ACX=XCB

Nie pomyliłeś środków?
8 maj 23:05
pie: UP
9 maj 22:19
pigor: .., widzę to np.tak: niech kąty w A,B,C to 2α,2β,2γ
odpowiednio dla ułatwienia zapisu , to
z tw. o kątach wpisanych opartych na tym samym łuku
o ΔBSD możemy powiedzieć, że
∡BDC=∡BAC= 2α i analogicznie
∡DBA=∡DCA=γ , ∡ABS=β ⇒ (*)
∡DBS=β+γ
a ponieważ
∡DSB=β+γ − jako kąt zewnętrzny ΔBSC,
a więc równy sumie kątów do niego nie przyległych, stąd
i z(*) ΔBSD − równoramienny i |BD|=|SD| c.n.w. . ...

9 maj 23:01

 To może ja też zrobię bo średnio mi wychodzi planimetria
To może ja też zrobię bo średnio mi wychodzi planimetria 
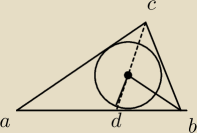
 Dobrze? Bo nie za bardzo wiedziałem gdzie ten D dać u góry czy na dole
Dobrze? Bo nie za bardzo wiedziałem gdzie ten D dać u góry czy na dole  bo w sumie może być też tak:
bo w sumie może być też tak:

 Jeśli już rysunek, to raczej tak.
Jeśli już rysunek, to raczej tak.

 mała podpowiedź?
mała podpowiedź?


 ACX=XCB
ACX=XCB  Nie pomyliłeś środków?
Nie pomyliłeś środków?
