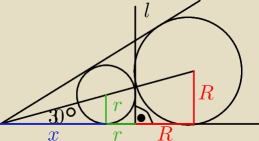
Ramiona kąta o mierze 60 przecięto prostą l prostopadłą do jednego z ramion. Nas pie: Ramiona kąta o mierze 60 przecięto prostą l prostopadłą do jednego z ramion. Następnie wpisano w ten kąt dwa koła, każde styczne do jego ramion i do prostej l. Wyznacz stosunek pól tych kół.

pie: UP

pigor: ... , niech r,R − długości promienia mniejszego koła i większego koła odpowiednio stycznych do wspólnej prostej, to

	PR		πR2		R
z warunków zadania (*)		=		= (		)2=?,
	Pr		πr2		r

	R−r		R−r
gdzie		= sin30o ⇔		= 12 ⇔ 2R−2r= R+r ⇔ R=3r ⇔
	R+r		R+r

	R		PR		R
⇔		= 3 stąd i z (*) ⇒		=(		)2= 32= 9 − szukany
	r		Pr		r

stosunek pól kół (lub odwrotnie) . ...

pie: Właśnie coś tu nie działa/niezbyt rozumiem treść zadania, bo odpowiedzi twierdzą, że to 7 − 4√3 lub 7 + 4√3.

Rajuu:

	1
a nie masz w odpowiedziach przypadkiem		?
	7−4√3

	1
bo mi wychodzi ładnie 7+4√3 i to jest równoważne		bo tak jak pigor napisał
	7−4√3

możemy wyliczyć stosunek koła większego do mniejszego albo mniejszego do większego

Rajuu:

	PR		πR2		R
Stosunek pól kół to tak jak pisał pigor		=		=(		)2 albo
	Pr		πr2		r

	Pr		r
		=(		)2
	PR		R

Uzależniam sobie x, R od zmiennej r

	√3
tg30=
	3

r		√3
	=
x		3

3r=√3x

	3r
x=		=√3r
	√3

a R liczę z Talesa:

R		R+r+√3r
	=
r		√3r

	(1+√3)2r
R=
	2

	R		(1+√3)2r		1
Teraz podstawiając do stosunku pól ({		)2=		*		)2=7+4√3
	r		2		r

Jak sobie zrobisz stosunek odwrotny to Ci te 7−√3 wyjdzie Ja napisałam w swoim wcześniejszym wejściu, że 7+4√3 = U{1}{7−4√3. Tylko, że to ten sam stosunek tylko inaczej zapisany, sorry za wprowadzenie w błąd

Rajuu:

	1
7+4√3=		*
	7−4√3

Rajuu: Kurcze, dopiero zaczynam swoją przygodę z pomaganiem i mam problemy z tymi kodami

	R		(1+√3)2r		1
Stosunek pól (		)2=(		*		)2=7+4√3
	r		2		r

Więcej zamętu wprowadziłam niż pomogłam

pigor: ..., kurde, tylko się zapić na ... przepraszam,

	R−r
powinno być		= tg30o (a nie sin30o), wtedy
	R+r

R−r		1		r (Rr −1		1
	=		⇔		=		⇔
R+r		√3		r (Rr +1)		√3

⇔ ^R_r√3−√3 = ^R_r +1 ⇔ ^R_r (√3−1) = √3+1 /*(√3+1) ⇔ ⇔ ^R_r (3−1) = 3+1+2√3 /:2 ⇔ ^R_r = 2+√3 ⇒ ⇒ P_R : P_r= (^R_r )²= (2+√3)²= 4+3+2√3= 7+2√3 i odwrotnie P_r : P_R= ( ^r_R)² = 1 : (7+√3) = 7−√3 . ....