aa
Hugo: Brothers, my time is over....
KTo robi Z "Hugusiem" −
Eta 
ostatnie zadanka przed jutrem

? Samemu smutno a
wrazie wątpliwości się poradzę. Do wygrania




8 maj 20:26
Marcin: Daj już spokój

Chociaż prezent przyjmę

8 maj 20:27
Hugo: #zadania są tylko typowo maturalne i prosze bez oszustw

rozwiaz nie równość |2x+4 | +|x−1|≤6
8 maj 20:27
Marcin: No to jedź przedziałami − bądźmy schematyczni

8 maj 20:30
Hugo:
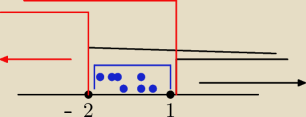
wysżło za 3 razem

<−3,1>
|2x+4 | +|x−1|≤6
1
o)
xe<1, oo) u xe{1}
2
o)
x≥−3 u xe <−oo, −2)
3
o)
xe(−2,1) u x≤1
Suma rozw:
<−3,1>
8 maj 20:46
Hugo: //sorki ze tak długo czasem

wyznacz wszystkie rozwiązania równania 2cos
2x−5sinx−4=0 dla przedziału <0,2pi>
8 maj 20:47
Marcin:
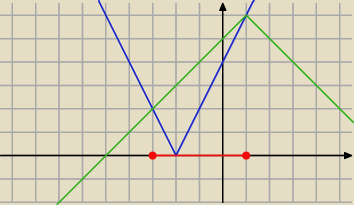
Brawo mistrzu

Masz graficznie jeszcze: (ja bym tak robił)
|2x+4|≤6−|x−1|
8 maj 20:50
Marcin: Hugo..
cos2x=1−sin2x, więc..
2(1−sin2x)−5sinx−4=0
8 maj 20:52
Hugo:
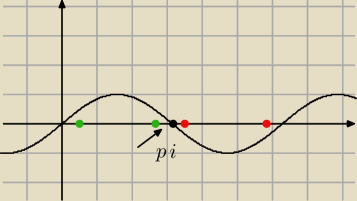
2cos
2x−5sinx−4=0
z jedynki tryg. //Hugo już wcześniej policzył dla tego delte

za dużo kawy
2(1−sin
2x)−5sinx−4=0
2−2sin
2−5sinx−4=0
−2sin
2−5sinx−2=0
t:=cosx //pytałem matematyczki to zmienna t nie jest wymagana

−2t
2−5t−2=0
2t
2+5t+2=0
Δ=25−16=9 // dobry znak

t= −5−3 /4 v t=−5+3/4
t=−4 (nie spełnia założeń sinusa) v t=−1/2
sinx=−0,5 //przedchwilą liczyłem dla sin
2x=−1/2 ....
//sinx=0,5 dla x=π/6 v x= 5/6π
π− 5/6π = 1/6π
| | 5 | |
x= π+1/6π=7/6π oraz x= 2π−π/6=1 |
| π |
| | 6 | |
JAKI TAM JEST SPÓJNIK

między tymi rozwiązaniami 'i' (daszek) czy 'lub' (v)
8 maj 21:01
Mila:
Przedziały:
1)
x<−2, wtedy mamy nierówność:
−2x−4+(−x+1)≤6⇔x≥−3 i x<−2
2) x∊<−2,1), wtedy mamy nierówność :
2x+4−x+1≤6⇔x≤1i x∊<−2,1)⇔x∊<−2,1)
3)x≥1 wtedy mamy nierówność:
2x+4+x−1≤6
3x≤3
x≤1 i x≥1⇔x=1
Łącznie
x∊<−3,1>
8 maj 21:01
Marcin: Ja nie daję żadnych znaków

x=..., x=... itd

Według mnie lepiej napisać, że cos(x)=t ∊<−1;1>
8 maj 21:03
Marcin: Mila.. Jak rozwiążę graficznie, do dostanę normalnie pełną ilość punktów, prawda?
8 maj 21:04
Hugo: Marcin musisz mi dawać czasu

to w odpowiedziach mam dobrze ale [C[prosze o komentarz do
postu]] 21:01 w ostatnim zapytaniu

#3
Bok kwadratu ABCD ma długosć 1 na boku BC i CD wybrano odpowiednio pkt E i F umieszone tak by
|CE|=|2DF|. Oblicz wartość x=|DF|, dla której pole trójkąta AEF jest namniejsza
8 maj 21:04
Hugo: przecinek jest równoznaczny z 'iloczynem' czyli daszkiem : >
8 maj 21:05
Marcin: No to ja daję daszek, ale nie wiem czy dobrze

8 maj 21:06
Mila:
Marcin, to zależy jakie zadanie, tu masz dokładne punkty przecięcia i możesz sprawdzić punkty
graniczne.
8 maj 21:08
Marcin: Ja wiem, ze jezeli nie da się odczytać, to trzeba liczyć, ale czasem wszystko ładnie widać i
szkoda czasu na obliczenia, w których mozna się pomylić

8 maj 21:09
Hugo:
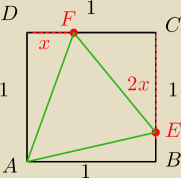
|CE|=|2DF|
Szukane: x=|DF|, dla której pole trójkąta AEF jest namniejsza
dajcie jeszcze chwilke

wyczuwam pitagorasa, będzie trzeba jedną zmienną, równanie
kwadratowe w postaci Pola kwadratu i pewnie wierzchołek

8 maj 21:14
Hugo: [Ż[Milo]] powiedz mi jak wychodzą mi z sinusów rozwiązania np.
sinx = a .... siny=b
to potem jak zapisuje
x=1...... x=2 ......x=3...... x=4 //lub (v) czy i ( daszek) między tymi wyrażeniami
8 maj 21:16
Marcin: Policz pola trzech trójkątów i odejmij je od pola kwadratu

8 maj 21:16
Nieuchwytny: Można również odjąć od pola kwadratu, pola trzech trójkątów.
8 maj 21:16
Mila:
Marcin, więc rozumiesz, że to trzeba z rozsądkiem wybrac sposób.
Hugo Wyjaśniam na przykładzie:
| | π | | 5 | |
x= |
| +2kπ lub x= |
| π+2kπ lub x=π+2kπ |
| | 6 | | 6 | |
8 maj 21:22
Hugo: czemu Pole a nie obwód... Pole Δ = ...
Zrobimy z tego śmiesznego wzoru Herona na Pole co nie ma czyżby w tablicach  ?
?
p=0,5p(a+b+c)
P=
√p(p−a)(p−b)(p−c)
Obliczamy długości miar trójkąta AFE
z tw. Pitagorasa
|AD|
2+|DF|
2 = |AF|
2
1
2+ x
2=|AF|
2
|AF|=
√12+x2
|FC|
2+|CE|
2=|FE|
2
(1−x)
2 + (2x)
2=|FE|
2
x2−2x+1+
4x2=|FE|
2
5x
2−2x+1=|FE|
2
|FE|=
√5x2−2x+1
|AE|
2=1
2+(1−2x)
2
|AE|
2=1+1+4x
2−4x
|AE|
2=2+4x
2−4x
|AE|=
√2+4x2−4x
BOKI:
|AE|=
√2+4x2−4x
|FE|=
√5x2−2x+1
|AF|=
√12+x2
//jak sie gdzieś pomyliłem krzyczcie wracam za 1,5min i dokańczam
Ale to jest paradoksalne że zadania za tę samą ilość pkt są nie takie same :c
8 maj 21:29
Hugo: Milo, Marcinie, Nieuchwytny każdy po


Miałem sie właśnei pytać czy jest inny sposób

Bede sie meczyć z Heronem

wasz jest szybszy ... kompne sie do waszego sposobu
8 maj 21:31
Nieuchwytny: W nagrodę masz zadanie W=cos15osin105o
8 maj 21:37
Hugo: zatem
P
Δ = P(kwadratu) − P1 − P2 − P3
P(1−3) − odpowiednio małe trójkąty
z tw. Pitagorasa
P1= x*1*0,5 = 0,5x
P2=(1−x)*2x*0,5=x−x
2 //
tu sie pomyliłem w miedzy czasie i mi wyszła f liniowa :C
| | 1−2x | |
P3=1* (1−2x)/2 = 1−2x/2 = |
| |
| | 2 | |
| | 1−2x | |
PΔ = 1 − 0,5x − (x−x2) − |
| |
| | 2 | |
| | 1−2x | |
PΔ =1 − 0,5x − x+x2 − |
| |
| | 2 | |
P
Δ =1 − 0,5x − x+x
2 − 0,5 + x
P
Δ = − 0,5x +x
2 +0,5
P
Δ = x
2 − 0,5x +0,5 //przemnożył bym ale sie boje

Z UWAGI ZE TO rosnąca F. KWADRATOWA (1:0 wróżbita Hugo

) najmniejszą wartość przyjmuje w
wierzchołku
p=−b/2a
p=0,25
//

Herbata mi mówi ze dobrze

8 maj 21:50
Mila:
No co Ty wyprawiasz?
| | 1 | |
PΔAEF=1−[ |
| *(1*x+(1−x)*2x+(1−2x)*1)] |
| | 2 | |
8 maj 21:53
Hugo: W=cos15cos105 //
Mnie na mięso?:c..... Niedoczekanie ! 
cos(60−45)sin(60+45)
(cos60cos45+sin60sin45 )(sin60cos45 + sin45cos60) //wyczuwam wzory skróconego mnoż.
| | √2 | | √3 | | √2 | | √3 | | √2 | | √2 | |
(0,5 * |
| + |
| * |
| ) ( |
| * |
| + |
| *0,5) |
| | 2 | | 2 | | 2 | | 2 | | 2 | | 2 | |
| | √2 | | √6 | | √6 | | √2 | |
( |
| + |
| ) ( |
| + |
| ) |
| | 4 | | 4 | | 4 | | 4 | |
| | 8 | |
W= |
| =0,5 //Dawaj jabłko Hugusiowi! btw. Ety nie ma dzisiaj :c? |
| | 16 | |
8 maj 22:00
MCC: jak masz rownanie, np wielomian (x+1)(x+7)(2x+3)=0
to piszesz lub (v) ( x=−1 v x=−7 v...)
jezeli opuszczasz wartosc bezwzgledna to w zaleznosci od tego czy mamy znak "<" czy ">" bedzie
odpowiednio "i" (daszek) oraz "lub" (v), dobrym patentem jest odwracanie tego zgodnie z
kieunkiem wskazowek zegara, juz tlumacze
jezeli < to np. |x+1| < 1
x+1<1 ⋀ x+1 > −1 (jak widac "<" jest godziną 9, poniej nasz daszek 12, a na koniec
mamy 3)
jezeli mamy > to np. |x+7|>5
x+7>5 v x+7<−5
czesto popelniane sa w tym bledy, a jest to wazne, poniewaz w jednym przypadku okreslamy czesc
wspolna, a w drugim sumujemy
8 maj 22:04
Nieuchwytny: źle

skorzystaj ze wzoru na połowę kąta

8 maj 22:04
Hugo: Milo przecież mam to samo... Przepraszam Cię jeżeli troche za bardzo brykam .. innym aspektem
jest to ze masz wszystko przerobione bardziej ode mnie przez to bardziej piszesz skrótowo ..
ja wole sb rozpisać bo po chwili popełniam błędy; zapominam minusa czy coś.
zw ide plum
8 maj 22:04
Marcin: Hugo, trzeba iść spać. Dobranoc

8 maj 22:05
Hugo: jaka ma być odpowiedź? Nieuchwytny
MCC: akurat nie chodzi o przedziały gdzie jest daszek i v... Ale dziękuję że miałeś ochotę tu
zerknąć

Sprawa tam się wyjaśniła z Milą i Marcinem, dajemy 'v' 'lub' między wynikami.
Generalnie umiem cały materiał tylko chwilami mam kryzysy. Proszę za życzliwość

8 maj 22:07
Hugo: Jeszcze godzine

I tak nie zasne ⇔ matma matma matma....
8 maj 22:08
Mila:
Nie było Twojego wpisu, a ja odchodziłam od komputera i dlatego Twoje rozwiązanie wcześniej się
pojawiło.
To pięknie, że sam dobrze rozwiązałeś.
Teraz idź spać, DOBRANOC
8 maj 22:09
8 maj 22:11
Nieuchwytny: W=cos15*sin105
W=cos15*sin(90+15)=cos15*cos15=cos
215
| | 30 | | 1+cos30 | | | |
cos15o=cos |
| =±√ |
| ±√ |
| =±√U{u{2+√3}}2 |
| | 2 | | 2 | | 2 | |
| | 2+√3 | | 1 | | 2+√3 | |
}=±√ |
| *±{ |
| }=±√ |
| |
| | 2 | | 2 | | 4 | |
| | 2+√3 | | 2+√3 | |
cos215o=(±√ |
| ) = |
| |
| | 4 | | 4 | |
8 maj 22:17
Nieuchwytny: Wyszły jakieś krzaczki. W ostatnim nawias jest do kwadratu.
8 maj 22:40
 ostatnie zadanka przed jutrem
ostatnie zadanka przed jutrem  ? Samemu smutno a
wrazie wątpliwości się poradzę. Do wygrania
? Samemu smutno a
wrazie wątpliwości się poradzę. Do wygrania 



 Chociaż prezent przyjmę
Chociaż prezent przyjmę 
 rozwiaz nie równość |2x+4 | +|x−1|≤6
rozwiaz nie równość |2x+4 | +|x−1|≤6

 wysżło za 3 razem
wysżło za 3 razem  <−3,1>
|2x+4 | +|x−1|≤6
1o)
xe<1, oo) u xe{1}
2o)
x≥−3 u xe <−oo, −2)
3o)
xe(−2,1) u x≤1
Suma rozw:
<−3,1>
<−3,1>
|2x+4 | +|x−1|≤6
1o)
xe<1, oo) u xe{1}
2o)
x≥−3 u xe <−oo, −2)
3o)
xe(−2,1) u x≤1
Suma rozw:
<−3,1>
 wyznacz wszystkie rozwiązania równania 2cos2x−5sinx−4=0 dla przedziału <0,2pi>
wyznacz wszystkie rozwiązania równania 2cos2x−5sinx−4=0 dla przedziału <0,2pi>
 Brawo mistrzu
Brawo mistrzu  Masz graficznie jeszcze: (ja bym tak robił)
|2x+4|≤6−|x−1|
Masz graficznie jeszcze: (ja bym tak robił)
|2x+4|≤6−|x−1|
 2cos2x−5sinx−4=0
z jedynki tryg. //Hugo już wcześniej policzył dla tego delte
2cos2x−5sinx−4=0
z jedynki tryg. //Hugo już wcześniej policzył dla tego delte  za dużo kawy
2(1−sin2x)−5sinx−4=0
2−2sin2−5sinx−4=0
−2sin2−5sinx−2=0
t:=cosx //pytałem matematyczki to zmienna t nie jest wymagana
za dużo kawy
2(1−sin2x)−5sinx−4=0
2−2sin2−5sinx−4=0
−2sin2−5sinx−2=0
t:=cosx //pytałem matematyczki to zmienna t nie jest wymagana  −2t2−5t−2=0
2t2+5t+2=0
Δ=25−16=9 // dobry znak
−2t2−5t−2=0
2t2+5t+2=0
Δ=25−16=9 // dobry znak  t= −5−3 /4 v t=−5+3/4
t=−4 (nie spełnia założeń sinusa) v t=−1/2
sinx=−0,5 //przedchwilą liczyłem dla sin2x=−1/2 ....
//sinx=0,5 dla x=π/6 v x= 5/6π
π− 5/6π = 1/6π
t= −5−3 /4 v t=−5+3/4
t=−4 (nie spełnia założeń sinusa) v t=−1/2
sinx=−0,5 //przedchwilą liczyłem dla sin2x=−1/2 ....
//sinx=0,5 dla x=π/6 v x= 5/6π
π− 5/6π = 1/6π
 między tymi rozwiązaniami 'i' (daszek) czy 'lub' (v)
między tymi rozwiązaniami 'i' (daszek) czy 'lub' (v)
 x=..., x=... itd
x=..., x=... itd  Według mnie lepiej napisać, że cos(x)=t ∊<−1;1>
Według mnie lepiej napisać, że cos(x)=t ∊<−1;1>
 to w odpowiedziach mam dobrze ale [C[prosze o komentarz do
postu]] 21:01 w ostatnim zapytaniu
to w odpowiedziach mam dobrze ale [C[prosze o komentarz do
postu]] 21:01 w ostatnim zapytaniu  #3
Bok kwadratu ABCD ma długosć 1 na boku BC i CD wybrano odpowiednio pkt E i F umieszone tak by
|CE|=|2DF|. Oblicz wartość x=|DF|, dla której pole trójkąta AEF jest namniejsza
#3
Bok kwadratu ABCD ma długosć 1 na boku BC i CD wybrano odpowiednio pkt E i F umieszone tak by
|CE|=|2DF|. Oblicz wartość x=|DF|, dla której pole trójkąta AEF jest namniejsza


 |CE|=|2DF|
Szukane: x=|DF|, dla której pole trójkąta AEF jest namniejsza
dajcie jeszcze chwilke
|CE|=|2DF|
Szukane: x=|DF|, dla której pole trójkąta AEF jest namniejsza
dajcie jeszcze chwilke  wyczuwam pitagorasa, będzie trzeba jedną zmienną, równanie
kwadratowe w postaci Pola kwadratu i pewnie wierzchołek
wyczuwam pitagorasa, będzie trzeba jedną zmienną, równanie
kwadratowe w postaci Pola kwadratu i pewnie wierzchołek 

 ?
p=0,5p(a+b+c)
P=√p(p−a)(p−b)(p−c)
Obliczamy długości miar trójkąta AFE
z tw. Pitagorasa
|AD|2+|DF|2 = |AF|2
12+ x2=|AF|2
|AF|=√12+x2
|FC|2+|CE|2=|FE|2
(1−x)2 + (2x)2=|FE|2
x2−2x+1+4x2=|FE|2
5x2−2x+1=|FE|2
|FE|=√5x2−2x+1
|AE|2=12+(1−2x)2
|AE|2=1+1+4x2−4x
|AE|2=2+4x2−4x
|AE|=√2+4x2−4x
BOKI:
|AE|=√2+4x2−4x
|FE|=√5x2−2x+1
|AF|=√12+x2
//jak sie gdzieś pomyliłem krzyczcie wracam za 1,5min i dokańczam
Ale to jest paradoksalne że zadania za tę samą ilość pkt są nie takie same :c
?
p=0,5p(a+b+c)
P=√p(p−a)(p−b)(p−c)
Obliczamy długości miar trójkąta AFE
z tw. Pitagorasa
|AD|2+|DF|2 = |AF|2
12+ x2=|AF|2
|AF|=√12+x2
|FC|2+|CE|2=|FE|2
(1−x)2 + (2x)2=|FE|2
x2−2x+1+4x2=|FE|2
5x2−2x+1=|FE|2
|FE|=√5x2−2x+1
|AE|2=12+(1−2x)2
|AE|2=1+1+4x2−4x
|AE|2=2+4x2−4x
|AE|=√2+4x2−4x
BOKI:
|AE|=√2+4x2−4x
|FE|=√5x2−2x+1
|AF|=√12+x2
//jak sie gdzieś pomyliłem krzyczcie wracam za 1,5min i dokańczam
Ale to jest paradoksalne że zadania za tę samą ilość pkt są nie takie same :c

 Miałem sie właśnei pytać czy jest inny sposób
Miałem sie właśnei pytać czy jest inny sposób  Bede sie meczyć z Heronem
Bede sie meczyć z Heronem  wasz jest szybszy ... kompne sie do waszego sposobu
wasz jest szybszy ... kompne sie do waszego sposobu
 Z UWAGI ZE TO rosnąca F. KWADRATOWA (1:0 wróżbita Hugo
Z UWAGI ZE TO rosnąca F. KWADRATOWA (1:0 wróżbita Hugo  ) najmniejszą wartość przyjmuje w
wierzchołku
p=−b/2a
) najmniejszą wartość przyjmuje w
wierzchołku
p=−b/2a
 Herbata mi mówi ze dobrze
Herbata mi mówi ze dobrze 
 cos(60−45)sin(60+45)
(cos60cos45+sin60sin45 )(sin60cos45 + sin45cos60) //wyczuwam wzory skróconego mnoż.
cos(60−45)sin(60+45)
(cos60cos45+sin60sin45 )(sin60cos45 + sin45cos60) //wyczuwam wzory skróconego mnoż.
 skorzystaj ze wzoru na połowę kąta
skorzystaj ze wzoru na połowę kąta 

 Sprawa tam się wyjaśniła z Milą i Marcinem, dajemy 'v' 'lub' między wynikami.
Generalnie umiem cały materiał tylko chwilami mam kryzysy. Proszę za życzliwość
Sprawa tam się wyjaśniła z Milą i Marcinem, dajemy 'v' 'lub' między wynikami.
Generalnie umiem cały materiał tylko chwilami mam kryzysy. Proszę za życzliwość 
 I tak nie zasne ⇔ matma matma matma....
I tak nie zasne ⇔ matma matma matma....