Na okręgu o promieniu 3 opisano trójkąt równoramienny o kącie między ramionami r
Grzegorz:
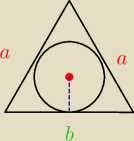
Na okręgu o promieniu 3 opisano trójkąt równoramienny o kącie między ramionami równym 120
o.
Oblicz długości boków tego trójkąta.
8 maj 20:02
Grzegorz: Na chwilę w trójkącie wyznaczyłem kąty 120o, 30o,30o jednak brakuje mi przynajmniej jednego
boku do policzenia pozostałych z funkcji tryg.
8 maj 20:04
BeforeU: Może z porownania pol
8 maj 20:16
BeforeU: albo inaczej

trojkat 60.30 . 90
8 maj 20:20
Grzegorz: Nic z tego nie wyliczę, bo r jest jedynie częścią jednego boku.
8 maj 20:21
BeforeU:
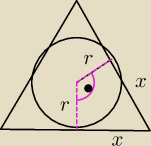
Moze cos z tego ?
8 maj 20:25
BeforeU: kAty proste powinny byc przy bokach

tam gdzie r prostopadle do boku
8 maj 20:27
BeforeU:
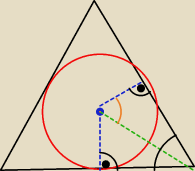
8 maj 20:39
Grzegorz: Zaraz dam tobie odpowiedź jak mi wychodzi.
8 maj 20:43
Grzegorz:
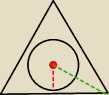
Wynik wychodzi błędny po zastosowaniu funkcji tryg. w powyższym przypadku. Masz jakiś inny
pomysł?
8 maj 21:06
Bogdan:

x
√3 = 3 ⇒ x =
√3 i y = 2x = 2
√3
a + x = 2(3 + y) ⇒ a = 6 + 4
√3 −
√3 = 6 + 3
√3
|AB| = 2a = 12 + 6
√3, |AC| = |BC| = a + x = ...
8 maj 21:09
Grzegorz: Wynik w wersji Bogdana wychodzi dobry, jednak nie rozumiem wszystkich zapisów. Mógłbyś
wytłumaczyć?
8 maj 21:18
Bogdan:
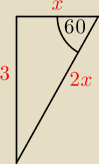
jeszcze raz: x
√3 = 3 ⇒ x =
√3
8 maj 21:29
 Na okręgu o promieniu 3 opisano trójkąt równoramienny o kącie między ramionami równym 120o.
Oblicz długości boków tego trójkąta.
Na okręgu o promieniu 3 opisano trójkąt równoramienny o kącie między ramionami równym 120o.
Oblicz długości boków tego trójkąta.
 trojkat 60.30 . 90
trojkat 60.30 . 90
 Moze cos z tego ?
Moze cos z tego ?
 tam gdzie r prostopadle do boku
tam gdzie r prostopadle do boku

 Wynik wychodzi błędny po zastosowaniu funkcji tryg. w powyższym przypadku. Masz jakiś inny
pomysł?
Wynik wychodzi błędny po zastosowaniu funkcji tryg. w powyższym przypadku. Masz jakiś inny
pomysł?
 x√3 = 3 ⇒ x = √3 i y = 2x = 2√3
a + x = 2(3 + y) ⇒ a = 6 + 4√3 − √3 = 6 + 3√3
|AB| = 2a = 12 + 6√3, |AC| = |BC| = a + x = ...
x√3 = 3 ⇒ x = √3 i y = 2x = 2√3
a + x = 2(3 + y) ⇒ a = 6 + 4√3 − √3 = 6 + 3√3
|AB| = 2a = 12 + 6√3, |AC| = |BC| = a + x = ...
 jeszcze raz: x√3 = 3 ⇒ x = √3
jeszcze raz: x√3 = 3 ⇒ x = √3