Planimetria, przekątne, pole czworokąta
Agre: Dany jest czworokąt ABCD, w którym długości boków wynoszą: |AB|=14, |CD|=30, |AD|=48 oraz kąty
DAB oraz BCD są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.
Podzieliłam figurę na dwa prostokątne trójkąty. I dzięki temu obliczyłam jedną z przekątnych
(BD), która jest równa 50. Bok BC z pitagorasa ma 40. Dodaje dwa P trójkątów i mam ostatecznie
wynik P=936j2
Nie wiem niestety jak obliczyć tę drugą przekątną AC, próbowałam ułożyć coś z twierdzeń
cosinusów, ale nie wychodziło mi nic.
Wiem z odp, że druga przekątna ma być równa= 46,8
Czy jest na to jakiś sposób?
8 maj 19:19
Tadeusz:
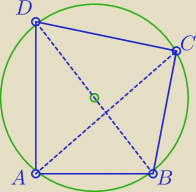
8 maj 19:35
Agre: Ja mogę stwierdzić, że okrąg mogę na nim opisać, czy to nie jest tak, że jeśli
α+γ=β+δ=180stopni
8 maj 19:38
Agre: ?
8 maj 19:38
Tadeusz:
... bo BD jest średnicą −

8 maj 19:55
Mateusz100: Jeżeli nie chcesz wyżej wymienionego sposobu to jest inny.
1.Liczysz cosinus kąta CDB, potem cosinus kąta ADB.
2.Liczysz z jedynki trygonometrycznej sinusy tych kątów
3.Liczysz cosinus sumy tych kątów ze wzoru cos(α+β) z tablic.
4.Tw. Cosinusów dla trójkąta DAC bo znasz cosinus kąta ADC i masz odpowiedź.
Może liczenia więcej ale tak też się da.
Btw: Możesz stwierdzić że da się opisać na tym trójkącie okrąg nie dlatego że BD jest średnicą
tylko dlatego że kąt DAB i DBC to kąty proste które sumują się do 180.
23 kwi 20:02
Eta:
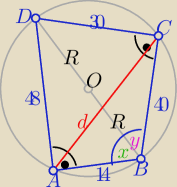
@
Mateusz100
Jak już "wykopałeś" zadanie sprzez 8 lat
to :
| | 1 | | 1 | |
|BD|=2R=50 P= |
| *30*40+ |
| *14*48 = 936 |
| | 2 | | 2 | |
z tw. sinusów wΔABC :
|AC|=d=2R*sin(x+y)
| | 48 | | 24 | | 14 | | 7 | | 3 | | 4 | |
sinx= |
| = |
| , cosx= |
| = |
| i siny= |
| , cosy= |
| |
| | 50 | | 25 | | 50 | | 25 | | 5 | | 5 | |
| | 117 | |
sin(x+y)=sinx*cosy+cosx*siny = ...........= |
| |
| | 125 | |
i po ptokach

23 kwi 21:59


 @Mateusz100
Jak już "wykopałeś" zadanie sprzez 8 lat
to :
@Mateusz100
Jak już "wykopałeś" zadanie sprzez 8 lat
to :
