| 3 | ||
mam dany sinα np. sinα = | i mam wyznaczyć cosα w tym przypadku muszę rozważyć dwie | |
| 7 |
| 3 | ||
sinα = | / ()2 | |
| 7 |
| 9 | ||
sin2α = | ||
| 49 |
| 9 | ||
1 − cos2α = | ||
| 49 |
| 9 | ||
cos2α = 1 − | ||
| 49 |
| 40 | ||
cos2α = | ||
| 49 |
| √40 | √40 | |||
cosα = | lub cosα = − | |||
| 7 | 7 |
 ? Bo gdy bym miał np. cosα a miał bym obliczyć sinα to wtedy sinα musi być dodatni i mam
tylko jedną możliwość. (oczywiście tyczy się to kąta np. w trójkącie)
? Bo gdy bym miał np. cosα a miał bym obliczyć sinα to wtedy sinα musi być dodatni i mam
tylko jedną możliwość. (oczywiście tyczy się to kąta np. w trójkącie)

 Zadanie 2
Sinusy kątów ostrych trójkąta prostokątnego oraz liczba 1 tworzą ciąg geometryczny. Oblicz
sinusa najmniejszego kąta tego trójkąta.
więc mam dane:
sinα,sinβ,1 −−−−−−−> zamieniam sinβ = cosα
sinα,cosα,1
są dwie możliwości :
sinα,cosα,1 v cosα,sinα,1 −−−> korzystam z własności ciągu i liczę :
cos2α = sinα v sin2α = cosα
z tego wychodzi mi że :
Zadanie 2
Sinusy kątów ostrych trójkąta prostokątnego oraz liczba 1 tworzą ciąg geometryczny. Oblicz
sinusa najmniejszego kąta tego trójkąta.
więc mam dane:
sinα,sinβ,1 −−−−−−−> zamieniam sinβ = cosα
sinα,cosα,1
są dwie możliwości :
sinα,cosα,1 v cosα,sinα,1 −−−> korzystam z własności ciągu i liczę :
cos2α = sinα v sin2α = cosα
z tego wychodzi mi że :
| −1−√5 | −1+ √5 | |||
sinα= | v sinα= | |||
| 2 | 2 |
| −1−√5 | −1+ √5 | |||
cosα= | v cosα= | |||
| 2 | 2 |

| −1 + √5 | ||
sinα = | (drugi odrzucamy bo < 0 więc α > 180o) | |
| 2 |
| −1 + √5 | √5 − 1 | |||
cosβ = | ⇒ sinβ = √ | |||
| 2 | 2 |
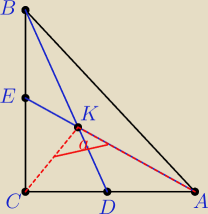 Zad.3 Dany jest trójkąt prostokątny równoramienny ABC o kącie prostym przy wierzchołku C.
Punkty D,E są środkami boków odpowiednio AC i BC. Odcinek AE i BD przecinają się w punkcie K.
Wyznacz sinusa kąta AKC.
sinα=?
wiem, że:
AC = BC = x oraz AB = x√2
Zad.3 Dany jest trójkąt prostokątny równoramienny ABC o kącie prostym przy wierzchołku C.
Punkty D,E są środkami boków odpowiednio AC i BC. Odcinek AE i BD przecinają się w punkcie K.
Wyznacz sinusa kąta AKC.
sinα=?
wiem, że:
AC = BC = x oraz AB = x√2
| x√5 | ||
z tw. pitagorasa AE = BD = | tyle wiem ale nie bardzo wiem jak to dalej ruszyć. | |
| 2 |
| 1 | ||
w podpowiedzi jest napisane że K dzieli BD i AE w stosunku | nie rozumiem dlaczego tak | |
| 3 |
 ?
?
| −1 + √5 | ||
dzięki, coś mi się ubzdurało że | jest mniejsze od 0  | |
| 2 |
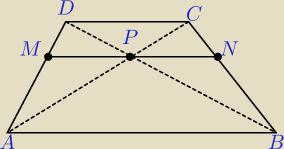 teraz ostatnie zadanko z dowodem:
Zadanie 4.
Przekątne trapezu ABCD przecinają się w punkcie P. Prosta równoległa do podstaw trapezu,
przechodząca przez punkt P, przecina ramiona AD i BC odpowiednio w punktach M i N.
Wykaż że MP = NP
Gdyby był to trapez równoramienny to nie miał bym problemu z uzasadnieniem, a tu nie bardzo
wiem jak sie za to zabrac. z góry dzięki za pomoc !
teraz ostatnie zadanko z dowodem:
Zadanie 4.
Przekątne trapezu ABCD przecinają się w punkcie P. Prosta równoległa do podstaw trapezu,
przechodząca przez punkt P, przecina ramiona AD i BC odpowiednio w punktach M i N.
Wykaż że MP = NP
Gdyby był to trapez równoramienny to nie miał bym problemu z uzasadnieniem, a tu nie bardzo
wiem jak sie za to zabrac. z góry dzięki za pomoc !
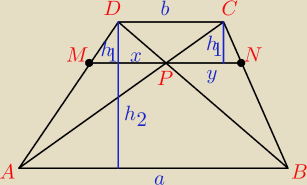 Z podobieństwa ABD (wys. to h2) i MPD (wys. to h1) mamy
Z podobieństwa ABD (wys. to h2) i MPD (wys. to h1) mamy
| x | h1 | ||
= | |||
| a | h2 |
| y | h1 | ||
= | |||
| a | h2 |