Ciekawe zadanko maturalne :D
Pat: W prawidłowym ostrosłupie trójkątnym ABCS poprowadzono płaszczyznę przechodzącą przez bok
podstawy AC = a i prostopadłą do krawędzi BS. Płaszczyzna przekroju odcina ostrosłup ABCD,
którego objętość jest równa 0,25 objętości ostrosłupa ABCS. Oblicz pole powierzchni całkowitej
ostrosłupa ABCS.
7 maj 17:58
Mila:
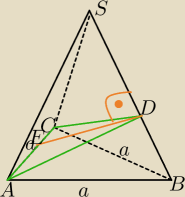
7 maj 19:22
Mila: ED⊥BS
Przekrój ACD podzielił ostrosłup ABCS na dwa ostrosłupy :
Możemy przyjąć, że
podstawą obu ostrosłupów jest ΔACD
Mamy ostrosłupy ACDS i ostrosłup ACDB
V− objętość ostrosłupa ABCS
| 3 | |
| V− objetość ostrosłupa ACDS (o wysokości DS) |
| 4 | |
| 1 | |
| V − objętość ostrosłupa ACDB ( o wysokości DB) |
| 4 | |
V
ACDS=3*V
ACDB⇔
| 1 | | 1 | |
| *PΔACD*|DS|=3* |
| *PΔACD*|DB|⇔ |
| 3 | | 3 | |
| | 1 | |
|DS|=3*|DB|⇔|DB|= |
| |BS| |
| | 4 | |
Pole Δ ABS:
AD⊥BS
| | 1 | | 1 | | 1 | |
P= |
| *|BS|*|AD| albo P= |
| a*hb= |
| *a*√BS2−(1/4)a2 |
| | 2 | | 2 | | 2 | |
=======================================================
Porównujemy pola trójkąta obliczone dwoma sposobami:
| 1 | | 1 | |
| *|BS|*|AD| = |
| *a*√BS2−(1/4)a2 gdzie: |
| 2 | | 2 | |
| | 1 | |
|AD|2=a2−|DB|2⇔|AD|2=a2−( |
| |BS|)2 |
| | 4 | |
| | 1 | |
|BS|*|AD| =a*√|BS|2−(1/4)a2 /2 ⇔|BS|2*|AD|2=a2*(|BS|2− |
| a2 |
| | 4 | |
| | 1 | | 1 | |
|BS|2*(a2− |
| |BS|2)=a2*(|BS|2− |
| a2 |
| | 16 | | 4 | |
stąd:
|BS|
2=2a
2
| | 1 | | 1 | |
PΔABS= |
| *a*√BS2−(1/4)a2= |
| a*√2a2−(1/4)a2 |
| | 2 | | 2 | |
| | 1 | | √7a2 | | a2√7 | |
PΔABS= |
| a* |
| = |
| |
| | 2 | | 2 | | 4 | |
====================
7 maj 20:10
Pat:
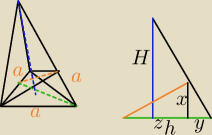
h =
a√32
x =
√zy
xy =
Hu{a√3{2}
7 maj 21:16
Mila:
Pat, jest zwyczaj, że się dziękuje za rozwiązanie.
7 maj 21:21
Pat: omg przepraszam cie najmocniej
sle calusy

7 maj 21:28
Pat: mam pewne watpliwosci jakby ktos mogl zobaczyc gdzie jest blad w moim rozumowaniu:
w odniesieniu do poprzedniego rysunku wynika ze x =
√3yH/2
V1 − objetosc ostroslupa mniejszego (tego na dole)
Vc − objetosc calego ostroslupa
V1 = ayH/4
V2 = a
2H
√3/12
Vc = 4 * V1 ⇒ y = a
√3/12 ⇒ z = a
√3/2 − a
√3/12 = 5a
√3/12
x =
√yz = a
√15/12 ⇒ H = x/y * a
√3/3 = a
√15/3
h − wysokość ściany bocznej
h
2 = H
2 + (a
√3/3)
2 ⇒ h =
√2a
Pc − pole całkowite
Pc = a
2√3/4 + 3 * 1/2 * a * a
√2
gdzie tu jest błąd ?


7 maj 21:38
Pat: a i oczywiscie z podobienstwa ⇒ x/y = H/a√3/3
7 maj 21:41
Mila:
Sposób dobry, ale ..
Trzeba pisać w jakich to trójkatach, bo trudno rozszyfrować co masz w głowie.
Nie sprawdzam dalej, ...
Skąd wzór na V1?
a
√2 to jest długość krawędzi bocznej
| | 1 | | a√3 | |
h2=H2+( |
| * |
| )2 wysokość ściany bocznej |
| | 3 | | 2 | |
7 maj 22:36

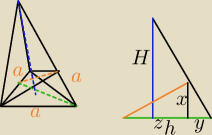 h = a√32
x = √zy
xy = Hu{a√3{2}
h = a√32
x = √zy
xy = Hu{a√3{2}


