funkcje + parametry + geometria
loitzl9006: Dla maturzystów − poziom R
Dana jest funkcja f(x)=mx−12√2. Dla jakich wartości parametru m miejsce zerowe x0 funkcji
f(x) przyjmuje taką wartość, że istnieje trójkąt prostokątny o przeciwprostokątnej długości 9
oraz przyprostokątnych długości m oraz 2x0+1 ?
Odp. m ∊ { 4√2; √26+√2 }
7 maj 15:07
muflon: x0=12√2/m
Z Pitagorasa:
92=m2+ [24√2+m/m]2
7 maj 15:44
zawodus: Dlaczego akurat w ten sposób?
7 maj 15:49
muflon: f(x) to funkcja liniowa
ax+b
x
0=−b/a
ok

7 maj 16:41
zawodus: Chodzi mi o skorzystanie z twierdzenia Pitagorasa
7 maj 16:52
muflon:
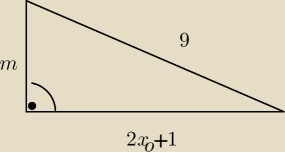
2x
0+1=2*12
√2/m +1=24
√2 + m/m= [(24
√2+m)/m]
7 maj 17:05
muflon: Zapomniałem wcześciej w nawiasie kwadratowym zapisać to ta, że jednoznacznie wynika, że w
liczniku jest 24√2+m
7 maj 17:07
zawodus: To policz do końca

7 maj 17:07
52: m
4 − 80m
2+48
√2m+1152=0
Jeśli się nie pomyliłem

7 maj 17:08
pigor: ...no to może coś takiego:
Hurtownik kupił 2 tony bananów.
45 bananów sprzedał z zyskiem12%,
a resztę sprzedał z zyskiem 5%. Na całej transakcji zarobił 424 zł. Ile
zapłacił za wszystkie banany.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
zad. z podręcznika do 1−szej Gimnazjum wyd. GWO oznaczone
szarą ◯ kropą , co oznacza "zadanie nieelementarne" jak piszą autorzy .

.
7 maj 17:14
zawodus: To jeśli jest ok to teraz Rozwiąż równanie
7 maj 17:15
muflon: przeczytałem wydawnictwo GMO i pomyślałem że może to ma cos wspólnego z tymi bananami

7 maj 17:16
pigor: ..., GWO (Gdańskie Wyd. Oświatowe), a nie GMO ,
a co do bananów, to ...

zadanie na czasie wszyscy
je jedzą, to i może coś w tym jest, że na maturze ...


7 maj 17:32
muflon: Sądzę, że zanim było to całe zamieszanie z Alvesem to dawno już arkusz był ułożony

7 maj 17:35
Domel: No mi wyłazi coś takiego:
m
4 − 80m
2 +48
√2m + 1152 = 0
−m
2(m−9)(m+9) = (m+24
√2)
2
Nie wiem co można z tego wysnuć dalej


7 maj 18:16
Domel: Odnośnie bananów − chyba założę hurtownię bo u mnie w rejonie sprzedam lepiej niż
po 2,24 zł/kg ( to ta cena z lepszym zyskiem

)
7 maj 18:43
ZKS:
No to wzory Ferriari.

m
4 − 80m
2 + 48
√2m + 1152 = 0
Budujemy równanie trzeciego stopnia
y
3 + 160y
2 + 1792y + 4608 = 0
wielomian zeruje y = −8
(y + 8)(y
2 + 152y + 576) = 0
y = −8 ∨ y = −76 − 20
√13 ∨ y = −76 + 20
√13
Szukamy tylko m > 0
| | √8 + √76 + 20√13 + √76 − 20√13 | |
m1 = |
| |
| | 2 | |
| | 2√2 + 5√2 + √26 + 5√2 − √26 | |
m1 = |
| |
| | 2 | |
m
1 = 4
√2
| | √8 − √76 + 20√13 − √76 − 20√13 | |
m2 = |
| |
| | 2 | |
| | 2√2 − 5√2 − √26 − 5√2 + √26 | |
m2 = |
| |
| | 2 | |
m
2 =
√2 +
√26
m
3 oraz m
4 są < 0.
7 maj 20:21
ZKS:
Oczywiście przy m
1 powinno być
| | −√8 + √76 + 20√13 + √76 − 20√13 | |
m1 = |
| |
| | 2 | |
7 maj 20:29
Domel: Ciekawe − czy to było z Ferrari Testarossa czy f12

i jakoś mało czerwonego koloru
7 maj 20:36
loitzl9006:
o nie, tego to ja się nie spodziewałem

ale chamsko to ułożyłem... jak by ułożył to równanie ze zmienną x
0 (a nie m) to by się obyło
bez tego wszystkiego, nie przewidziałem że jak równanie 4−go stopnia z m będzie to takie
kwiatki się pojawią...
m
2+(2x
0+1)
2=81
| 288 | |
| +4x02+4x0−80=0 |*x02 |
| x02 | |
4x
04+4x
03−80x
02+288=0 || :4
x
04+x
03−20x
02+72=0
i widać że x
0=−2 jest pierwiastkiem, dzielimy przez (x
0+2):
(x
0+2)(x
03−x
02−18x
0+36)=0
pierwiastkiem tego drugiego jest x
0=3
x
0=−2 ⋁ (x
0−3)(x
02+2x
0−12)=0
x
0=−2 ⋁ x
0=3 ⋁ x
02+2x
0−12=0
x
02+2x
0−12=0
Δ=4−4*1*(−12)=52 →
√Δ=2
√13
| | −2−2√13 | |
x01= |
| =−1−√13 → nie spełnia warunków zadania |
| | 2 | |
x
02=−1+
√13
2x
0+1 > 0 ⇔ x
0=3 ⋁ x
0=−1+
√13
dla x
0=3,
dla x
0=−1+
√13
| | 12√2 | | 12√2*(√13+1) | |
m= |
| = |
| = |
| | √13−1 | | (√13−1)(√13+1) | |
7 maj 20:53
ZKS:
Ewentualnie wpadł mi taki pomysł.
m4 − 80m2 +48√2m + 1152 = 0
m4 − 4m2 + 4 − 76m2+ 48√2m + 1148 = 0
(m2 − 2)2 − 50m2 + 100√2m − 100 − 26m2 − 52√2m − 52 + 1300 = 0
(m − √2)2(m + √2)2 − 50(m − √2)2 − 26(m + √2)2 + 1300 = 0
[(m + √2)2 − 50](m − √2)2 − 26[(m + √2)2 − 50] = 0
[(m + √2)2 − 50][(m − √2)2 − 26] = 0
7 maj 21:03
Domel: O kurde

O w morde − zgłoszę to do Nobla
7 maj 21:15
Vizer: Heh
ZKS widzę, że nie wypadłeś z formy

7 maj 21:16
Domel: Ja już to wydrukowałem i szukam ramki, żeby postawić na telewizorze

7 maj 21:23
zawodus: ZKS nawet pamiętasz, kto wymyślił sposób na równania 4 stopnia

Ja ich nigdy nie pamiętam

chyba dlatego że ich nie używam

7 maj 21:30
Vizer: Akurat Ferrari się łatwo kojarzy

7 maj 21:32
pigor: ...,Hurtownik kupił 2 tony bananów. 45 bananów sprzedał z zyskiem12%,
a resztę sprzedał z zyskiem 5%. Na całej transakcji zarobił 424 zł.
Ile zapłacił za wszystkie banany.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
..., np. tak ; niech
x = ? − ile zapłacił hurtownik za banany,
to
45*12%x+ 15*5%x= 424 ⇔ 0,8*012x+0,2*0,05x= 424 ⇔
⇒ 0,096x+0,010x= 424 ⇔ 0,106x= 424 ⇔
x= 4240,106=
4000 [zł].

7 maj 22:53
Hugo: Jutro z wami siadam nad matmą...

Wychodzi mi po zmaganiach z kalkulatorem (angielski)
+90% z podstawy
77−80% z rozszerzenia zakładając że poszła super rozprawka

(3 za 3 przeciw dość bogate
słownictwo i 248 słów)
7 maj 22:58
pigor: ..., no to może jeszcze sprawdzę ten zysk:
(0,8*1,12+0,2*1.05)*
4000= (0,896+0,21)*4000= 1,106*4000=
4424 zł.

7 maj 23:20
Hugo: Ile waży banan?
0,12% * 45 + (x−45)0,05 = 424
5,4 + 0,05x − 5,4=424
0,05x =424
x=8480
7 maj 23:31
Eta:
Jaki?

dojrzały ? czy zielony?

7 maj 23:32
Hugo: 
Eta !
nie rozumiem zadania mamy:
dwie tony: 2000kg => 45 bananów + reszta
[kg]= [postać nie mianowana] + [coś tam XD] <= ale chyba też postać nie mianowana
Postać jest na tyle urojona że te kg muszę się znosić

To będzie I prawo Huga

7 maj 23:36
bezendu:
Hugo nie podlizuj się !
Eta jest w 1 klasie LO

7 maj 23:42
Hugo: II*

7 maj 23:43
Domel: Hugo a ta postać to w kapeluszu czy berecie

− bo już się zgubiłem.
I ile sztuk bananów ta postać sprzedaje/kupuje

7 maj 23:46
Hugo: Hugo czeka na koniec matur a potem bedzie nawracać

Bezendu spraw bym miał słuszność

JUż mi jest obojętne na studia ale zobaczyć mine
nauczycielki która nigdy we mnie nie wierzyła i uważała za nieudolnego :c
100≥a>b>
√9025
a− twoja matura
b − moja
7 maj 23:47
Hugo: Domel: Ktoś wrzucił zadanie Hugo nie ogarnął xd ale nie mogę się wypowiadać tutaj bo nie jestem
autorem

7 maj 23:48
Domel: A w ogóle i szczególe proponuję nadać nazwę postaci np.
Hugotek 
a nie tak ciągle
„niemianowana”
7 maj 23:48
Hugo: 
Eta mi mówi Huguś

...

8 maj 00:03

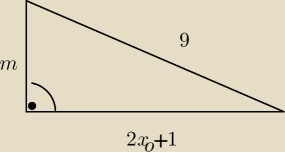 2x0+1=2*12√2/m +1=24√2 + m/m= [(24√2+m)/m]
2x0+1=2*12√2/m +1=24√2 + m/m= [(24√2+m)/m]


 .
.

 zadanie na czasie wszyscy
je jedzą, to i może coś w tym jest, że na maturze ...
zadanie na czasie wszyscy
je jedzą, to i może coś w tym jest, że na maturze ... 




 )
)
 m4 − 80m2 + 48√2m + 1152 = 0
Budujemy równanie trzeciego stopnia
y3 + 160y2 + 1792y + 4608 = 0
wielomian zeruje y = −8
(y + 8)(y2 + 152y + 576) = 0
y = −8 ∨ y = −76 − 20√13 ∨ y = −76 + 20√13
Szukamy tylko m > 0
m4 − 80m2 + 48√2m + 1152 = 0
Budujemy równanie trzeciego stopnia
y3 + 160y2 + 1792y + 4608 = 0
wielomian zeruje y = −8
(y + 8)(y2 + 152y + 576) = 0
y = −8 ∨ y = −76 − 20√13 ∨ y = −76 + 20√13
Szukamy tylko m > 0
 i jakoś mało czerwonego koloru
i jakoś mało czerwonego koloru
 ale chamsko to ułożyłem... jak by ułożył to równanie ze zmienną x0 (a nie m) to by się obyło
bez tego wszystkiego, nie przewidziałem że jak równanie 4−go stopnia z m będzie to takie
kwiatki się pojawią...
ale chamsko to ułożyłem... jak by ułożył to równanie ze zmienną x0 (a nie m) to by się obyło
bez tego wszystkiego, nie przewidziałem że jak równanie 4−go stopnia z m będzie to takie
kwiatki się pojawią...
 O w morde − zgłoszę to do Nobla
O w morde − zgłoszę to do Nobla


 Ja ich nigdy nie pamiętam
Ja ich nigdy nie pamiętam  chyba dlatego że ich nie używam
chyba dlatego że ich nie używam 


 Wychodzi mi po zmaganiach z kalkulatorem (angielski)
+90% z podstawy
77−80% z rozszerzenia zakładając że poszła super rozprawka
Wychodzi mi po zmaganiach z kalkulatorem (angielski)
+90% z podstawy
77−80% z rozszerzenia zakładając że poszła super rozprawka  (3 za 3 przeciw dość bogate
słownictwo i 248 słów)
(3 za 3 przeciw dość bogate
słownictwo i 248 słów)

 dojrzały ? czy zielony?
dojrzały ? czy zielony? 
 Eta !
nie rozumiem zadania mamy:
dwie tony: 2000kg => 45 bananów + reszta
[kg]= [postać nie mianowana] + [coś tam XD] <= ale chyba też postać nie mianowana
Postać jest na tyle urojona że te kg muszę się znosić
Eta !
nie rozumiem zadania mamy:
dwie tony: 2000kg => 45 bananów + reszta
[kg]= [postać nie mianowana] + [coś tam XD] <= ale chyba też postać nie mianowana
Postać jest na tyle urojona że te kg muszę się znosić  To będzie I prawo Huga
To będzie I prawo Huga 


 − bo już się zgubiłem.
I ile sztuk bananów ta postać sprzedaje/kupuje
− bo już się zgubiłem.
I ile sztuk bananów ta postać sprzedaje/kupuje 
 Bezendu spraw bym miał słuszność
Bezendu spraw bym miał słuszność JUż mi jest obojętne na studia ale zobaczyć mine
nauczycielki która nigdy we mnie nie wierzyła i uważała za nieudolnego :c
100≥a>b> √9025
a− twoja matura
b − moja
JUż mi jest obojętne na studia ale zobaczyć mine
nauczycielki która nigdy we mnie nie wierzyła i uważała za nieudolnego :c
100≥a>b> √9025
a− twoja matura
b − moja

 a nie tak ciągle
„niemianowana”
a nie tak ciągle
„niemianowana”
 Eta mi mówi Huguś
Eta mi mówi Huguś  ...
...