okręgi.. kolorado : Na okręgu o promieniu 2 opisano trapez równoramienny o polu 20.Olicz długość boków trapezu.

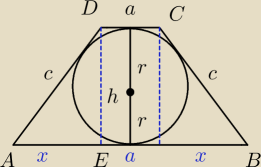
Vizer: r = 2 P = 20 h = 2r = 4

	b −a
x =
	2

Z własności czworokąta opisanego na okręgu : 2c = a + b Z pola wynika :

	1
20 =		(a + b) * 4
	2

10 = a + b (*) 10 = 2c c = 5 Z twierdzenia Pitagorasa dla trójkąta ADE : h² + x² = c² 16 + x² = 25 x² = 9 x = 3

b − a
	= 3
2

b − a = 6 b = a + 6 (**) Z (*) i (**) => 10 = 2a + 6 => a = 2 i b = 8

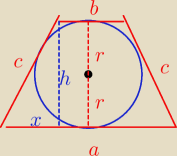
Janek191: P = 0,5*( a + b)*h = 20 h = 2 r = 2*2 = 4 więc 0,5*(a + b)*4 = 20 a + b = 10 = 2 c ⇒ c = 5 x² = c² − h² = 25 − 16 = 9 x = 3

a − b
	= x = 3 ⇒ a − b = 2*3 = 6
2

Mamy a + b = 10 a − b = 6 −−−−−−−−−−−−−− 2a = 16 a = 8 ==== b = a − 6 = 2 ========== c = 5 ====

kolorado: Vizer mógłbyś wytłumaczyć mi zależność x=b−a/2

Vizer: Oczywiście : b = 2x + a 2x = b − a

	b − a
x =
	2

omamo: dziękuje

omamo: ...w imieniu siostry bo już poszła xddd

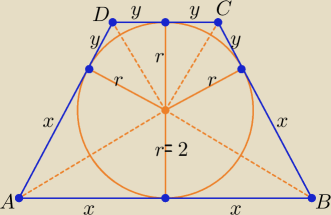
Bogdan: 2r(x + y) = P i xy = r² ⇒ 4(x + y) = 20 i xy = 4 ⇒ y = 5 − x i x(5 − x) = 4 x² − 5x + 4 = 0 ⇒ (x − 1)(x − 4) = 0 ⇒ x = 1 i y = 4 lub x = 4 i x = 1 Odp.: Dla x > y: |AB| = 2x = 8, |CD| = 2y = 2, |BC| = |AD| = x + y = 5