wykres funkcji kwadratowej Zagubiona: Naszkicuj wykres funkcji f(x)=x²−2x−3. Podaj miejsca zerowe, współrzędne wierzchołka, punkt przecięcia z osią OX, przedziały monotoniczności funkcji. Wyszło mi tak, że: miejsca zerowe to −4 i 1 Przedział monotoniczności to x∊(−∞;−4)u(1;+∞) Ramiona są skierowane ku górze. Nie wiem jak obliczyć współrzędne wierzchołka. A punkt przecięcia z osią OX to też −4 i 1?

J: Wszystko żle..

Zagubiona: To mnie nie pocieszyłeś... to jak ja powinnam to zrobić?

Zagubiona: Przecież wyliczyłam p=−4 q=1

J: Napisałaś,że to miejsca zerowe.. , a nawet jeśli to p i q ... to również źle.

Zagubiona: więc co powinnam obliczyc by było dobrze?

J: Zacznij od miejsc zerowych, czyli policz Δ, potem x₁ i x₂

Zagubiona: Δ=16 a jaki jest wzór na x₁ i x₂?

J:

	−b + √Δ		−b − √Δ
x1 =		, x1 =
	2a		2a

Zagubiona: x₁=3 x₂=−1

J: Teraz policz p i q

Zagubiona: p= ^−b_2a = ²₂ = 1 q = ^−Δ_4a = ⁻¹⁶₄ = −4

J: Dobrze... Punkty przecięcia z osią OX to miejsca zerowe. W zadaniu pewnie chodziło o to, aby podać punkt przecięcia z osia OY .... zatem policz f(0)

Zagubiona: Zadanie brzmi dokładnie tak jak napisałam i jest z osią OX. Może to podchwytliwe? A miejsca zerowe to x₁ i x₂? A współrzędne wierzchołka to p i q?

J: Tak.. Została monotoniczność ... dla jakich x parabola opada w dół, dla jakich idzie do góry ?

Zagubiona: hm... w dół idzie od (−∞; −1) a w góre (3;+∞) ?

Zagubiona: Dobrze?

J: Maleje ( − ∞,1) , rosnie (1,+∞)

Zagubiona: Dlaczego wszystko sprowadza się do 1?

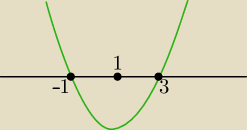
J: Teraz widzisz ...?

Zagubiona: Yhym, czyli znaleźliśmy liczbę pośrodku −1 i 3? Tak? I tak ma wyglądać ten wykres?

J: x = 1 to współrzędna wierzchołka paraboli

Zagubiona: Czyli to p, a q to co?

J: Druga współrzędna wierzchołka: W(p,q)