Nierówności wymierne gabaa:

x4+x2+1
	<0
x2−4x−5

ja: Dziedzina ! (x⁴+x²+1)(x²−4x−5)<0⇔x²−4x−5<0 rozwiązać

5-latek: zalozenie x²−4x−5≠0 rozwiaz to z alozenia masz juz postac iloczynowa teraz rozwiaz x⁴+x²+1=0 tez dostaniesz postac iloczynowa Zobacz moze sie cos skroci Potem skorzystaj z tego ze znak ilorazu jest taki sam jak iloczynu (chodzi o znak a nie wartosc i zamiem iloraz na iloczyn masz juz nierownosc wielomianowa ata juz potrafisz rozwiazac

J: Cześć 5−latek... , przeoczyłeś,że licznik jest zawsze dodatni..

muflon: gabaa z Reja?

5-latek: Czesac J Powiem CI ze nawet sie nad tym nie zastanawialem .Nie rozwiazywalem tego . Pokazalem sposob ogolny . Wiesz ja lubie rozwiazywac zadanka jak ten sztachanowiec . czyli duzo sie narobic

gabaa: Dziękuję

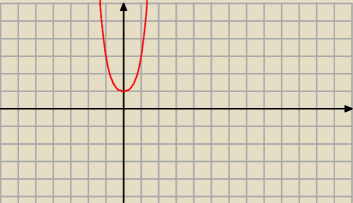
5-latek: to jewst wykres funkcji y=x⁴+x²+1 Widzisz ze lezy on nad osia OX wiec to wyrazenie x⁴+x²+1 bedzie zawsze dodatnie Teraz tak . Jesli licznik jest dodatni to zeby cale wyrazenie wymieerne bylo ujemne czyli <0 wiec mianownik musi byc <0

ja: wystarczy x²=t >0 wtedy t²+t+1 nie ma miejsc zerowych w zbiorze liczb Rzeczywistych i nie istnieje t−1 i t₂ Wystarczy