trapez równoramienny katB: W trapezie równoramiennym, przekątna o długości 3√2 tworzy z krótszą podstawą kąt 45^o, a z ramieniem 75^o. Oblicz obwód trapezu, oraz obwód okręgu na nim opisanego.

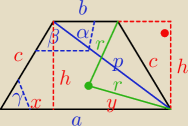
Janek191: p = 3√2 α = 45^o β = 75^o więc α + β = 120^o zatem γ = 60^o oraz mamy p = 3√2 ⇒ h = 3

h		3		√3
	=		= sin 60o =		⇒ c √3 = 3*2 ⇒ c = 2√3
c		c		2

x		x		1
	=		= cos 60o =		⇒ x = √3
c		2√3		2

y² = p² − h² = (3√2)² − 3² = 18 − 9 = 9 y = 3, więc a = x + y = √3 + 3 b = a − 2 x = 3 + √3 − 2*√3 = 3 − √3 Obwód trapezu L = a + b + 2 c = √3 + 3 + 3 − √3 + 2*2√3 = 6 + 4√3 =========================================== r² = 6 ⇒ r = √6 więc obwód koła opisanego na trapezie L₁ = 2π*r =2√6 π =================

katB: Tak samo mi wyszło. Dzięki wielkie