ułamki algebraiczne jellyfish: 1. Suma wszystkich rozwiązań równania (x−3)(x−2)(x+1)(2x−3)/2x2−9x+9=0 wynosi: A. 1 B. 5 1/2 C.10 D. 4 2/3 (odp A) 2. Dane jest równanie ⁵_x −a²=2x z niewiadomą z, gdzie x≠0. Liczba 1/2 jest rozwiązaniem tego równania wtedy i tylko wtedy, gdy: A. a=3 B. a=−3 C.a2= 1.5 D. a∊ {−3,3} (odp D) 3. Wykres funkcji F(x)= 2/x przesunięto o 3 jednostki w lewo wzdłuż osi OZ i otrzymano wykres funkcji G. Zatem: A. G(x) = ²_x −3 B. G(x)= ²_x−3 C.G(x)= ²_x+3 D.G(x)= ²_x +3 (odp C) 4. Zbiorem wartości funkcji F(x) = ⁵_x −1 jest zbiór: A. R−{0} B.R−{5} C.R−{−1} D.R−{1} (odp C) 5.Miejscem zerowym funkcji F(x) = ³_x+5 −2 jest liczba: A. −3 ¹₂ B. −5 C. −2 D. 6 ¹₂ (odp A)

Janek191: z.1 2 x² − 9 x + 9 = 0 Δ = 81 − 4*2*9 = 81 − 72 = 9 √Δ = 3

	9 − 3		9 + 3
x =		= 1,5 lub x =		= 3
	4		4

Dziedzina równania : R \ { 1,5 ; 3} Rozwiązania równania: x₁ = 2 x₂ = − 1 zatem suma x₁ + x₂ = 2 − 1 = 1 Odp. A ========

Janek191: z.5

5
	− a2 = 2 x ; x ≠ 0
x

1
	= 0,5 jest rozwiązaniem równania, więc
2

5
	− a2 = 2*0,5
0,5

10 − a² = 1 a² = 9 a = − 3 lub a = 3 a ∊ { − 3; 3 } =========

Janek191: To było z.2

Janek191: z.3 y = U{2]{x} ; x ≠ 0 → v = [ − 3 ; 0 ] więc

	2		2
y =		+ 0 =
	x − (−3)		x + 3

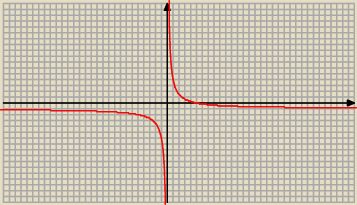
Janek191: z.4

	5
f(x) =		− 1
	x

więc ZWf = R \ { − 1} Patrz też wykres.

Janek191: z.5 x ≠ − 5

	3		3		2*( x+5)
f(x) =		− 2 =		−		=
	x + 5		x + 5		x + 5

	− 2 x − 7
=		= 0 ⇔ x = − 3,5
	x + 5