prawdopodobienstwo P@weł: Zrobi mi ktos to zadanie sposobem drzewka BARDZO PROSZE! W zielonym pudełku jest 10 monet o nominale 5zł i 5 monet o nominale 2 zł, a w białym 2 monety o nominale 5 zł i 3 monety o nominale 2 zł. Z zielonego pudełka losujemy jedną monetę i wrzucamy ją do białego. Następnie z białego pudełka wyciągamy 2 monety. Oblicz prawdopodobieństwo wylosowania z białego pudełka łącznie 7 zł.

P@weł: umiem zrobić jedynie tak:

10
	− czyli 10 monet 5−złotowych na 15 monet wszystkich
15

5
	= czyli 5 monet 2 złotowych na 15 monet wszystkich
15

A w białym pudełku analogicznie ....

P@weł: "?

P@weł: "?

P@weł: I jak, ktos chetny do pomocy

Alfa:

P@weł:

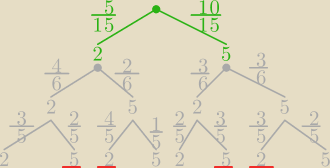
	2
Nie rozumiem dlaczegi jest dalej po zielonej 2−ce ułamek
	6

A moglby ktos pokazac jak bedzie wygladalo to zadnie sposobem na kombinacje?

loitzl9006: dlatego, że jak wylosujesz 2zł z zielonego, to przekładasz je do białego, i w białym jest już

	2
6 monet: cztery 2zł i dwie 5 zł, stąd
	6

sposób "z kombinacji"

	5		4 1   2 1   *		10		3 1   3 1   *
P =		*		+		*		=
	15		6 2		15		6 2

	26
		(wychodzi tyle samo co z powyższego drzewka, więc chyba dobrze jest )
	45

	5
Czyli tak: szansa		że monetą z zielonego pudełka będzie 2zł. W białym pudełku jest więc
	15

	6 2
już 6 monet. Losujemy 2 monety z 6 z białego pudełka dlatego w mianowniku jest		, i

	4 1		2 1
szansa że wylosujemy po jednej 5zł i 2zł jest równa		*		(jedną z czterech 5zł i

jedną z dwóch 2zł)

	10
Analogiczne rozumowanie możesz zrobić dla drugiej części (tej z		)
	15