Prawdopodobieństwo
P@weł: Witam! Mógłby mi ktoś dać jakieś zadania na poziomie matury rozszerzonej z prawdopodobieństwa
i rozwiązać sposobem "drzewka" (no i mniejwiecej wytlumaczyc co robimy)

Nie rozumiem jak
sie robi tym sposobem a bym chcial zrozumiec

5 maj 18:02
P@weł: bardzo prosze

5 maj 18:37
Donbi: Drzewka na maturze rozszerzonej? Czemu chcesz sobie tak utrudniać?
5 maj 18:55
razor: W zielonym pudełku jest 10 monet o nominale 5zł i 5 monet o nominale 2 zł, a w białym 2 monety
o nominale 5 zł i 3 monety o nominale 2 zł. Z zielonego pudełka losujemy jedną monetę i
wrzucamy ją do białego. Następnie z białego pudełka wyciągamy 2 monety. Oblicz
prawdopodobieństwo wylosowania z białego pudełka łącznie 7 zł.
zadanko chyba dobrze wszystkim znane

5 maj 18:58
Arcctg: Ogolnie z drzewkami chodzi o to, że suma prawdopodobieństw na jednym poziomie gałęzi musi
wynosić 1. I gdy masz już narysowane drzewko to okreslone prawdopodobieństwo liczysz w ten
sposób, że mnożysz prawdopodobieństwa na wszystkich poziomach gałęzi(wybierasz sobie jakby
"ścieżke"[Zdarzenie, które Cię interesuje] której prawdopodobieństwa mnożysz.
5 maj 19:01
Arcctg: Ogolnie z drzewkami chodzi o to, że suma prawdopodobieństw na jednym poziomie gałęzi musi
wynosić 1. I gdy masz już narysowane drzewko to okreslone prawdopodobieństwo liczysz w ten
sposób, że mnożysz prawdopodobieństwa na wszystkich poziomach gałęzi(wybierasz sobie jakby
"ścieżke"[Zdarzenie, które Cię interesuje] której prawdopodobieństwa mnożysz.
5 maj 19:01
Arcctg: Ogolnie z drzewkami chodzi o to, że suma prawdopodobieństw na jednym poziomie gałęzi musi
wynosić 1. I gdy masz już narysowane drzewko to okreslone prawdopodobieństwo liczysz w ten
sposób, że mnożysz prawdopodobieństwa na wszystkich poziomach gałęzi(wybierasz sobie jakby
"ścieżke"[Zdarzenie, które Cię interesuje] której prawdopodobieństwa mnożysz.
5 maj 19:02
Draghan:
 Donbi
Donbi, to wcale nie są aż takie utrudnienia

Pewnie dostanie mi się od
PW, jak to zobaczy, ale trudno

To np. takie zadanie:
W urnie znajduje się 5 kul białych i 6 kul czarnych. Losujemy 2 razy bez zwracania po jednej
kuli.
Oblicz prawdopodobieństwo, że obie kule będą różnych kolorów.
Ogólnie drzewko można sobie machnąć, jak jest tak do trzech losowań i nie ma za dużej puli
możliwych wyników, inaczej wychodzą jakieś dżungle, a nie drzewka

Podstawa, to poprawnie opisać to drzewko.
P@weł, chyba wiesz, na czym to polega?

A liczenie to banał − każdą osobną gałąź mnożysz, a poszczególne gałęzie − dodajesz

| | 5 | | 6 | | 6 | | 5 | |
P(A) = |
| * |
| + |
| * |
| |
| | 11 | | 10 | | 11 | | 10 | |
5 maj 19:11
P@weł: Draghan , rozumiem do momentu środkowego , pozniej jakos nie moge załapać ...
| | 6 | |
U{5]{11} To 5 kul białych z 11 wszyskich , po prawej |
| to 6 czarnych z 11 wszystkich |
| | 11 | |
i nie zbyt rozumiem dalej co zrobiłes?
Co potem oznaczaja rozbite na 2 gałęzie , lewa strona i prawa strona...

5 maj 20:14
P@weł: Razor, co do twojego zadania to se nie poradze, wytlumaczysz jak zrobic je drzewkiem?
5 maj 20:19
Draghan: Nie wiem, o co Ci chodzi, bo strasznie zamotałeś

Ale pewnie chodzi o samą konstrukcję tego
"drzewka".
Najpierw Ci napiszę trochę, jak "interpretować" drzewko. Każdy możliwy wynik losowania, to
"przejście" od korzenia (kropa u góry) aż na sam dół, idąc po linii. Np. jednym z wyników jest
ta gałąź, zaznaczona na niebiesko, gdzie najpierw losujemy kulę białą, a później czarną.
To zabieramy się za rysowanie. Po kolei. Najpierw robimy "korzeń" i z niego wyprowadzamy jedno
losowanie. Możemy wylosować kulę białą lub czarną, a więc 2 możliwe wyniki, dwie gałęzie.
| | 5 | |
Na wylosowanie białej mamy |
| szans (bo białych kul jest 5, a wszystkich kul jest 11), a |
| | 11 | |
| | 6 | |
na wylosowanie czarnej |
| . |
| | 11 | |
Rysujemy drugie losowanie. Teraz dla każdej z gałęzi, które narysowaliśmy, dorysowujemy kolejne
możliwe wyniki losowania. Czyli dla każdej gałęzi wynikiem kolejnego losowania może być kula
biała lub czarna.
Teraz trzeba opisać. Będę teraz pisał od lewej strony, po kolei. Na wylosowanie drugiej białej
| | 4 | |
kuli masz |
| szans, bo białych kul zostało Ci 4, a wszystkich zostało 10 (bo w pierwszym |
| | 10 | |
losowaniu wyjąłeś jedną białą...).
| | 6 | |
Dalej: na wylosowanie czarnej, masz |
| szans, ponieważ w urnie znajduje się 6 czarnych |
| | 10 | |
kul (poprzednio wyjąłeś jedną białą). I dalej analogicznie.
Jak opisujesz, zawsze musisz mieć w głowie, jaka zawartość Ci zostaje do dyspozycji.
Teraz przeanalizuj, co napisałem i zrób kilka zadań, a nabierzesz wprawy

Aaaaargh, umre tu, próbując to wysłać


5 maj 20:36
P@weł:
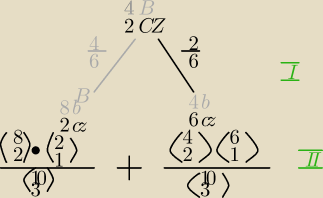
Naprawde nie rozumiem sposobu twojego tłumaczenia, bardziej zrozumiałe jest mi to zadania
W urnie znajduja sie 4 kule białe i 2 czarne . Losujemy jedna kule i zwracamy ja do urny wraz z
4 dodatkowymi kulami tego samego koloru co kula wylosowana. nasteonie losujemy 3 kule. Jakie
jest prawdopodobienstwo ze w drugim losowaniu otrzymamy 2 kule białe i 1 czarna.
Naprawde łatwiej mi jest zrobic te zadanie niz twoje .
U ciebie nie rozumiem tego jak to logicznie dla mnie rozpisac : "" Losujemy 2 razy bez
zwracania po jednej kuli. Oblicz prawdopodobieństwo, że obie kule będą różnych kolorów "
5 maj 21:21
Draghan: Przykro mi, lepiej Ci nie wytłumaczę

I nie wiem, czego nie rozumiesz w poleceniu

Przecież jasne, jak słoneczko: masz pudło, w nim
kulki w dwóch kolorach, bierzesz losowo dwie z nich, a chcesz wylosować dwie różnokolorowe
kulki

5 maj 21:24
P@weł: mi sie zdaje ze ty pokreciles cos z liczeniu wyniku
| | 5 | | 6 | |
Dlaczego mnożysz |
| * |
| skoro według zadania wybierałeś 2 kule rózne ( czyli |
| | 11 | | 10 | |
jedna czarna i druga biała)
chyba powinno być:
| 5 | | 4 | | 5 | | 6 | |
| * |
| + |
| * |
| |
| 11 | | 10 | | 11 | | 10 | |
5 maj 22:10
P@weł: mi sie zdaje ze ty pokreciles cos z liczeniu wyniku
| | 5 | | 6 | |
Dlaczego mnożysz |
| * |
| skoro według zadania wybierałeś 2 kule rózne ( czyli |
| | 11 | | 10 | |
jedna czarna i druga biała)
chyba powinno być:
| 5 | | 4 | | 6 | | 5 | |
| * |
| + |
| * |
| |
| 11 | | 10 | | 11 | | 10 | |
5 maj 22:11
P@weł: wpis " 5 maj 22:11" jest poprawny w poprzednim pomylilem ułamki
5 maj 22:13
 Nie rozumiem jak
sie robi tym sposobem a bym chcial zrozumiec
Nie rozumiem jak
sie robi tym sposobem a bym chcial zrozumiec 


 Donbi, to wcale nie są aż takie utrudnienia
Donbi, to wcale nie są aż takie utrudnienia  Pewnie dostanie mi się od PW, jak to zobaczy, ale trudno
Pewnie dostanie mi się od PW, jak to zobaczy, ale trudno  To np. takie zadanie:
W urnie znajduje się 5 kul białych i 6 kul czarnych. Losujemy 2 razy bez zwracania po jednej
kuli.
Oblicz prawdopodobieństwo, że obie kule będą różnych kolorów.
Ogólnie drzewko można sobie machnąć, jak jest tak do trzech losowań i nie ma za dużej puli
możliwych wyników, inaczej wychodzą jakieś dżungle, a nie drzewka
To np. takie zadanie:
W urnie znajduje się 5 kul białych i 6 kul czarnych. Losujemy 2 razy bez zwracania po jednej
kuli.
Oblicz prawdopodobieństwo, że obie kule będą różnych kolorów.
Ogólnie drzewko można sobie machnąć, jak jest tak do trzech losowań i nie ma za dużej puli
możliwych wyników, inaczej wychodzą jakieś dżungle, a nie drzewka  Podstawa, to poprawnie opisać to drzewko.
P@weł, chyba wiesz, na czym to polega?
Podstawa, to poprawnie opisać to drzewko.
P@weł, chyba wiesz, na czym to polega?  A liczenie to banał − każdą osobną gałąź mnożysz, a poszczególne gałęzie − dodajesz
A liczenie to banał − każdą osobną gałąź mnożysz, a poszczególne gałęzie − dodajesz 

 Ale pewnie chodzi o samą konstrukcję tego
"drzewka".
Najpierw Ci napiszę trochę, jak "interpretować" drzewko. Każdy możliwy wynik losowania, to
"przejście" od korzenia (kropa u góry) aż na sam dół, idąc po linii. Np. jednym z wyników jest
ta gałąź, zaznaczona na niebiesko, gdzie najpierw losujemy kulę białą, a później czarną.
To zabieramy się za rysowanie. Po kolei. Najpierw robimy "korzeń" i z niego wyprowadzamy jedno
losowanie. Możemy wylosować kulę białą lub czarną, a więc 2 możliwe wyniki, dwie gałęzie.
Ale pewnie chodzi o samą konstrukcję tego
"drzewka".
Najpierw Ci napiszę trochę, jak "interpretować" drzewko. Każdy możliwy wynik losowania, to
"przejście" od korzenia (kropa u góry) aż na sam dół, idąc po linii. Np. jednym z wyników jest
ta gałąź, zaznaczona na niebiesko, gdzie najpierw losujemy kulę białą, a później czarną.
To zabieramy się za rysowanie. Po kolei. Najpierw robimy "korzeń" i z niego wyprowadzamy jedno
losowanie. Możemy wylosować kulę białą lub czarną, a więc 2 możliwe wyniki, dwie gałęzie.
 Aaaaargh, umre tu, próbując to wysłać
Aaaaargh, umre tu, próbując to wysłać 

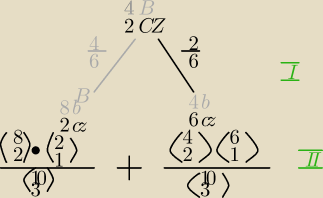 Naprawde nie rozumiem sposobu twojego tłumaczenia, bardziej zrozumiałe jest mi to zadania
W urnie znajduja sie 4 kule białe i 2 czarne . Losujemy jedna kule i zwracamy ja do urny wraz z
4 dodatkowymi kulami tego samego koloru co kula wylosowana. nasteonie losujemy 3 kule. Jakie
jest prawdopodobienstwo ze w drugim losowaniu otrzymamy 2 kule białe i 1 czarna.
Naprawde łatwiej mi jest zrobic te zadanie niz twoje .
U ciebie nie rozumiem tego jak to logicznie dla mnie rozpisac : "" Losujemy 2 razy bez
zwracania po jednej kuli. Oblicz prawdopodobieństwo, że obie kule będą różnych kolorów "
Naprawde nie rozumiem sposobu twojego tłumaczenia, bardziej zrozumiałe jest mi to zadania
W urnie znajduja sie 4 kule białe i 2 czarne . Losujemy jedna kule i zwracamy ja do urny wraz z
4 dodatkowymi kulami tego samego koloru co kula wylosowana. nasteonie losujemy 3 kule. Jakie
jest prawdopodobienstwo ze w drugim losowaniu otrzymamy 2 kule białe i 1 czarna.
Naprawde łatwiej mi jest zrobic te zadanie niz twoje .
U ciebie nie rozumiem tego jak to logicznie dla mnie rozpisac : "" Losujemy 2 razy bez
zwracania po jednej kuli. Oblicz prawdopodobieństwo, że obie kule będą różnych kolorów "
 I nie wiem, czego nie rozumiesz w poleceniu
I nie wiem, czego nie rozumiesz w poleceniu  Przecież jasne, jak słoneczko: masz pudło, w nim
kulki w dwóch kolorach, bierzesz losowo dwie z nich, a chcesz wylosować dwie różnokolorowe
kulki
Przecież jasne, jak słoneczko: masz pudło, w nim
kulki w dwóch kolorach, bierzesz losowo dwie z nich, a chcesz wylosować dwie różnokolorowe
kulki 