Pomóżcie prosze..
Julka ;) :) ;*: Rozwiaz rownanie |8x
3−1| = x − 8x
2 Bardzo prosze o rozwiazanie bo nie wiem czy robie
dobrze a za chwile matura

wynik to ; równanie sprzeczne
4 maj 20:17
Julka ;) :) ;*: pomocy..
4 maj 20:20
Marcin:
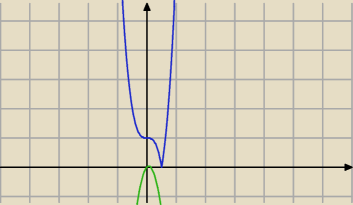

wynik
4 maj 20:20
ICSP: sprzeczne
4 maj 20:21
5-latek:
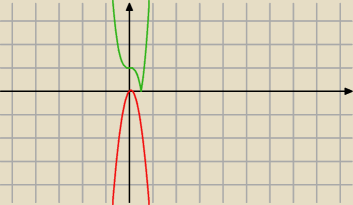
takie sa wykresy tych dwoch funkcji
4 maj 20:21
zawodus: wynik ok

Wykres
Marcina coś nie tak

4 maj 20:22
Marcin: Czemu?

Takie mi tutaj narysowało

4 maj 20:23
zawodus: Dobra idę spać

4 maj 20:24
ICSP:
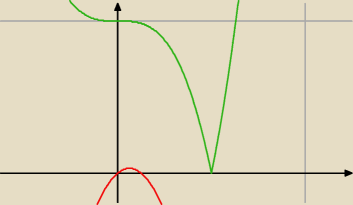
4 maj 20:24
Marcin: Tez chyba idę

4 maj 20:26
Julka ;) :) ;*: bylby ktos tak mily i rozwiazal mi to.. ?
4 maj 20:28
ICSP: a wkład własny ?
4 maj 20:30
Julka ;) :) ;*: Mam tak
4 maj 20:31
Julka ;) :) ;*: rozbilam bezwzgledna z wzoru skroconego mnozenia a3−b3
wyszlo mi (2x−1)(4x2+2x+1)
4 maj 20:33
Julka ;) :) ;*: z tego jest tylko jeden pierwiastek 1/2
4 maj 20:33
ICSP: 
zatem przedziały w których będziesz rozpatrywać swoją nierówność ?
4 maj 20:34
Julka ;) :) ;*: i z drugiego wyciagnelam x(8x−1) i tu mam pierwiastki 0 i 1/8
4 maj 20:34
Julka ;) :) ;*: i wlasnie z tego drugiego tez cos wyciagam czy nie

4 maj 20:35
Julka ;) :) ;*: i wlasnie z tego drugiego tez tworze przedzialy czy nie?
4 maj 20:35
sushi_ gg6397228:
po co komplikujesz
rysujesz y=8x3
potem przesuwasz o 1 w dół
działasz wartością bezwzględną i po problemie
druga strona−−> to wiadomo 2 miejsca zerowe , parabola itp
4 maj 20:36
Julka ;) :) ;*: druga strona czyli z x−8x2 tez wyciagam pierwiastki?
4 maj 20:38
Julka ;) :) ;*: prosze powiedzcie
4 maj 20:40
zawodus: tak

jeśli interesuje cię graficzne rozwiązanie

4 maj 20:42
Julka ;) :) ;*: interesuje mnie rozwiazanie z wytlumaczeniem..

4 maj 20:57
5-latek: Dla jakiego x |8x3−1| sie zeruje ?
4 maj 21:00
zawodus: julka żądasz wyjaśnień i tłumaczeń. Denerwujesz się, ale takie rzeczy było pytać rok temu.
Teraz to trochę późno.
4 maj 21:10
PW: Lewa strona równania jest dla dowolnej x liczbą nieujemną. Nie ma więc sensu szukanie rozwiązań
tam, gdzie prawa strona jest ujemna. Ograniczmy zatem poszukiwanie rozwiązań do takich x, dla
których
x − 8x
2 ≥ 0
| | 1 | |
Widać, że rozwiązań zadanego równania należy szukać na przedziale [0, |
| ]. |
| | 8 | |
Lewa strona równania na tym przedziale jest równa
|8x
3 − 1| = |(2x)
3 − 1| = |(2x−1)(4x
2+2x+1)| = −(2x−1)(4x
2+2x+1) = −8x
3 + 1.
Ostatnia równość wynika stąd, że 2x−1 < 0 i 4x
2+2x+1 > 0 (na ustalonym przedziale wyrażenie
8x
3 − 1 jest ujemne, a więc jego moduł jest równy liczbie przeciwnej).
Pozostaje rozwiązać równanie
| | 1 | |
− 8x3 + 1 = −x − 8x2, x∊ [0, |
| ]. |
| | 8 | |
8x
3 − 8x
2 − x − 1 = 0
| | 1 | |
8x2(x−1) + (−x−1) = 0, x∊ [0, |
| ]. |
| | 8 | |
Jak łatwo zauważyć równanie to nie ma rozwiązań − oba składniki po lewej stronie są ujemne.
Odpowiedź: Badane równanie nie ma rozwiązań.
4 maj 21:21
Julka ;) :) ;*: i bardzo dziekuje
4 maj 21:35
mietek: rozwiązanie
PW piękne, ale i tak tego nie zrozumiesz

4 maj 21:37
Julka ;) :) ;*: Kumam wiec mnie tu nie obrazaj co?
4 maj 21:58
mietek: powodzenia na maturce w takim razie jak wszystko "kumasz"
4 maj 22:01
 wynik to ; równanie sprzeczne
wynik to ; równanie sprzeczne

 wynik
wynik
 takie sa wykresy tych dwoch funkcji
takie sa wykresy tych dwoch funkcji
 Wykres Marcina coś nie tak
Wykres Marcina coś nie tak 
 Takie mi tutaj narysowało
Takie mi tutaj narysowało



 zatem przedziały w których będziesz rozpatrywać swoją nierówność ?
zatem przedziały w których będziesz rozpatrywać swoją nierówność ?

 jeśli interesuje cię graficzne rozwiązanie
jeśli interesuje cię graficzne rozwiązanie 

