Ladnie prosze o pomoc Julka ;) :) ;*: rozwiąż rownanie | X³ − x | + X² − 1 = 0 czy moze mi ktos wytlumaczyc jak w takim czyms sie opuszcza bezwzgledna? i jak sie z tego uklada przedzialy? Prosze o pomoc

Julka ;) :) ;*: ja tez w potrzebie xd

Draghan: Ładnie prosisz o pomoc ^w^ Pewnie musisz ustalić miejsca zerowe wyrażenia w module i rozstrzygnąć, na jakie przedziały podzielić dalszy etap rozwiązania... x³ − x = 0 (...)

Draghan: Ups, coś mi tam jakieś krzaczki wyskoczyły Miał być uśmiech ładny dla Ciebie, a nie takie straszydła ^w^

Julka ;) :) ;*: no dobra tyle wiem ...ale jak to sie robi?

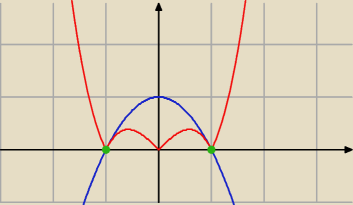
Marcin: Tutaj masz wyniki jak na dłoni, ale niestety na maturze tak łatwo wykresu nie narysujesz

Julka ;) :) ;*: Wiec... serio ;3 niech mi ktos wytlumaczy prosze

Draghan: Kurczę, już miałem napisane, ale usunąłem Poczekaj moment, to Ci rozpiszę

Marcin: |x³ − x| + x² − 1 =0 |x³ − x|=−x²+1 teraz z tego masz: x³ − x=−x²+1 ← rozwiąż x³ − x=x²−1 ← i to też

Marcin: ehh wybacz Draghan, ze Ci się wbiłem w rozwiązanie

Draghan: x³ − x = 0 x(x² − 1) = 0 (1) x = 0 (2) x² − 1 = 0 x² = 1 x = 1 v x = −1 I teraz rysujesz wykres i układasz przedziały. Z rysunku widać, że rozpatrywane przedziały to będą: (1) (−oo; −1) − moduł ujemny (2) <−1; 0) − moduł dodatni (3) <0; 1) − moduł ujemny (4) <1; +oo) − moduł dodatni

Draghan: No, pokrzyżowaliśmy się trochę Ale to nic Smacznego piwka

Marcin: Po co Ci taka zabawa z przedziałami? Dziękuję

Draghan: Bo nigdy nie liczyłem takich zadań A co, nie wyjdzie mi tak?

Marcin: Wyjdzie, ale jest więcej roboty

Julka ;) :) ;*: czyli tak fajnie mam bezwzgledna juhu rozpisuje jak ty ....sprawdzam jak to leci czy gora czy dolem rysuje sobie tego wezyka i mam przedzialy tak?

zawodus: Julka miałaś do mnie pisać

Draghan: No to skoro wyjdzie... A Juleczka prosiła o sposób... Twój szybszy, ale nie na wszystkie takie zadanka działa... Jakby miała np. dwa niezależne moduły? Wtedy mój sposób ma przewagę

Marcin: hahaha zawodus sobie nadzieję zrobił

Draghan: Tak, Julka − o to chodzi

Marcin: Tak, wtedy Twój sposób ma przewagę

Julka ;) :) ;*: ale marcin jesli mozesz powiedz mi tylko ...jak zamienisz to co napisales na wielomianowa ..to pozniej zaznaczam te punkty wszytkie?

Marcin: Jak zamienię to co napisałem na wielomianową? nie rozumiem

Julka ;) :) ;*: znaczy dostane pierwiastki

Marcin: No tak. To co Ci wyjdzie, to będą rozwiązania do zadania Próbuj sposobem Draghana, jest bardziej schematyczny, takze sobie potrenujesz

Julka ;) :) ;*: Dobra dziekuje

zawodus: Jeden moduł to leci rozwiązywanie bez przedziałów. Dwa i więcej to przedziały. Najszybszy sposób to liczenie w pamięci

Draghan: Napisz do zawodusa, On Ci pomoże...

Draghan: O, sam do Ciebie pisze

Julka ;) :) ;*: jeszcze jedno powiedzcie mi prosze ....jak w rownaiu dojsc czy idzie gora czy dolem ten wezyk Oo

Marcin: Podstaw sobie np 100 i zobacz czy wartość jest wtedy dodatnia czy ujemna. Ja tak przynajmniej robię

Julka ;) :) ;*: swoja droga mam do niego napisac chyba na numer IP xd

Marcin: haha dobre

Marcin: Nawet powiem Ci, ze jest taka możliwość

Draghan: Zależy od systemu, na jakim nerduje zwaodus

Draghan: pracuje* przepraszam, literówka

Marcin: dodaj jeszcze, ze celowa

Draghan: