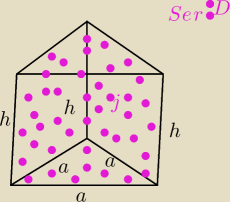
 objętość graniastosłupa prawidłowego trójkątnego jest równa 12√3 a pole powierzchni bocznej
tego graniastosłupa jest równe 36. Oblicz sinus kąta jaki tworzy rzekątna ściany bocznej z
sąsiednią ścianą boczna.
V = Pp*h=12√3
Pb=3*h*a = 36
objętość graniastosłupa prawidłowego trójkątnego jest równa 12√3 a pole powierzchni bocznej
tego graniastosłupa jest równe 36. Oblicz sinus kąta jaki tworzy rzekątna ściany bocznej z
sąsiednią ścianą boczna.
V = Pp*h=12√3
Pb=3*h*a = 36
| a2√3 | ||
12√3 = | *h | |
| 4 |
| 12 | ||
12=h*a ⇔ a= | ||
| h |
| |||||||||||
12√3 = | *h | ||||||||||
| 4 |
| ||||||||
12√3 = | *h /dzielimy przez √3 | |||||||
| 4 |
| 36 | ||
12 = | *h | |
| h2 |
| 36 | ||
12 = | ||
| h |
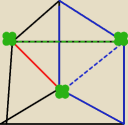 Oblicz sinus kąta jaki tworzy przekątna ściany bocznej z
sąsiednią ścianą boczna.
nie ogarniam dobrze mam ?
Oblicz sinus kąta jaki tworzy przekątna ściany bocznej z
sąsiednią ścianą boczna.
nie ogarniam dobrze mam ?
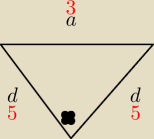 Jezeli to mam dobrze to bedzie:
z pitagorasa
a2+h2=d2
9+16=25
d=55
Pewnie macie lepsze pomysły ale dałbył z tw. cosinusów a potem z jedynki tryg
Jezeli to mam dobrze to bedzie:
z pitagorasa
a2+h2=d2
9+16=25
d=55
Pewnie macie lepsze pomysły ale dałbył z tw. cosinusów a potem z jedynki tryg
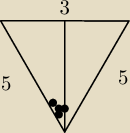 d=5**
tw cos
32=25+25−25cosα
9=50−25cosα
41=25cosα
d=5**
tw cos
32=25+25−25cosα
9=50−25cosα
41=25cosα
| 41 | ||
cosα = | ||
| 25 |
 nowa myśl:
nowa myśl:
| 1,5 | 3 | |||
sinα'= | = | |||
| 5 | 10 |

 ale jak po patrze to bede wiedzieć
ale jak po patrze to bede wiedzieć
| 41 | ||
cosα= | ||
| 50 |
| 41 | ||
( | )2 +sin2α=1 | |
| 50 |
| 1681 | |
+sin2α=1 | |
| 2500 |
| 819 | ||
sin2a= | ||
| 2500 |
| 3√91 | ||
sinα= | ||
| 50 |
 Jutro polski (nie piszesz?
Jutro polski (nie piszesz?  )
)
 Angielski musze ogarnac w końcu coś nie mam kiedy
Angielski musze ogarnac w końcu coś nie mam kiedy