Dla maturzystów
Domel: Dla maturzystów
Rozwiąż nierówność:
||x2 − 5| + 4| > 8
3 maj 21:16
zawodus: fajne

, bo dużo znaczków, a niektóre można usunąć

3 maj 21:17
muflon: x2−5 wyznaczasz miejsca miejsca zerowe i badasz znak
rozwiązujesz dalej w przedziałach
3 maj 21:19
ICSP: ||x2 − 5| + 4| > 8
|x2 − 5| > 4
(x2 − 5 − 4)(x2 − 5 + 4) > 0
(x−3)(x−1)(x+1)(x+3) > 0
x ∊ (− ∞ ; − 3) ∪ (−1 ; 1) ∪ (3 ; + ∞)
3 maj 21:20
zawodus: O znalazł się
maturzysta 
3 maj 21:21
Marcin: No nie ma sensu rozwiązywanie |x
2−5|+4 < −8

a na maturze by to większość liczyła

3 maj 21:23
zawodus: W ogóle ta linijka "nie powinna" się pojawić

, bo
||x
2−5|+4|=|x
2−5|+4

3 maj 21:25
muflon: a no fakt, ale ze mnie żal

3 maj 21:29
Domel: muflon − nie bądź taki pesymista − jak byś robił konsekwentnie swoim sposobem to też byś
dostał prawidłowy wynik

3 maj 21:33
ICSP: masz coś jeszcze dla maturzystów ?

3 maj 21:36
rina: marcin dlaczego nie ma sensu

z zalozenia ze IaI=−a jest nieprawdziwe

3 maj 21:36
Marcin: Po lewej stronie masz wartość bezwzględną + 4, co jest zawsze dodatnie. Po lewej masz liczbę
ujemną −8. Czy −8 może być kiedykolwiek większe od liczby dodatniej?
3 maj 21:38
3 maj 21:53
Marcin: Jakby nie polski, to pewnie bym zajrzał

3 maj 21:54
ICSP: Stereometrii wole nie ruszać

3 maj 21:54
Domel: No to geometria

Wykazać, że w trójkącie równoramiennym suma odległości dowolnego punktu podstawy od ramion
trójkąta jest równa odległości wierzchołka podstawy od przeciwległego boku
3 maj 21:57
ICSP: Nie masz czegoś z równań ?

3 maj 21:58
razor:
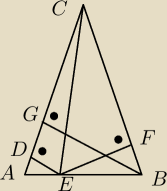
PΔABC = 1/2*|AC|*|GB|
PΔABC = PΔAEC + PΔBEC = 1/2*|AC|*|DE| + 1/2*|BC|*|EF| = 1/2*|AC|*(|DE|+|EF|)
|DE| + |EF| = |GB|
ckd
3 maj 22:03
Domel: 
3 maj 22:05
razor: 
3 maj 22:08
Domel:
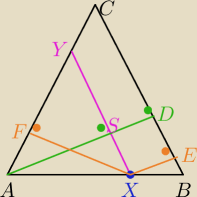
Ale lepiej widać chyba tu:
odcinek XY || BC => |XE| = |SD| ∧ |XF| = |AS|
więc
|XE| + |XF| = |AD|
3 maj 22:11
Domel: No to równanko
Dla jakich wartości parametru k równanie:
x2 − 2x − k2 −1 = 0
ma dwa pierwiastki x1 i x2 takie, że
x1∊(1+√6; 1+√11) i |x1 − x2| < 6
3 maj 22:20
 , bo dużo znaczków, a niektóre można usunąć
, bo dużo znaczków, a niektóre można usunąć 

 a na maturze by to większość liczyła
a na maturze by to większość liczyła 
 , bo
||x2−5|+4|=|x2−5|+4
, bo
||x2−5|+4|=|x2−5|+4




 z zalozenia ze IaI=−a jest nieprawdziwe
z zalozenia ze IaI=−a jest nieprawdziwe


 Wykazać, że w trójkącie równoramiennym suma odległości dowolnego punktu podstawy od ramion
trójkąta jest równa odległości wierzchołka podstawy od przeciwległego boku
Wykazać, że w trójkącie równoramiennym suma odległości dowolnego punktu podstawy od ramion
trójkąta jest równa odległości wierzchołka podstawy od przeciwległego boku

 PΔABC = 1/2*|AC|*|GB|
PΔABC = PΔAEC + PΔBEC = 1/2*|AC|*|DE| + 1/2*|BC|*|EF| = 1/2*|AC|*(|DE|+|EF|)
|DE| + |EF| = |GB|
ckd
PΔABC = 1/2*|AC|*|GB|
PΔABC = PΔAEC + PΔBEC = 1/2*|AC|*|DE| + 1/2*|BC|*|EF| = 1/2*|AC|*(|DE|+|EF|)
|DE| + |EF| = |GB|
ckd


 Ale lepiej widać chyba tu:
odcinek XY || BC => |XE| = |SD| ∧ |XF| = |AS|
więc
|XE| + |XF| = |AD|
Ale lepiej widać chyba tu:
odcinek XY || BC => |XE| = |SD| ∧ |XF| = |AS|
więc
|XE| + |XF| = |AD|