Prawdopodobieństwo BlueJ: Mamy dane P(A)= 0,6, P(B')=0,3. Należy wykazać, że P(A ∩ B) ≥0,3. Wiem, że mogę to rozwiązać w ten sposób: P(A∪B) = P(A)+P(B)− P(A∩ B) P(A∪B) = 0,6+0,7− P(A∩B) P(A∪B) = 1,3− P(A∩B) i P(A∪B)≤1 1,3− P(A∩B)≤1 P(A∩B) ≥ 0,3 Ale kombinowałam (na podstawie rysunku dwóch zbiorów ze wspólną cześcią) i wyszło mi coś takiego : P(A)+P(B')= 1− P(B)+ P(A∩ B) 0,6 + 0,3= 1− 0,7+ P(A∩ B) P(A∩ B)= 0,6 I stąd mam pytanie czy wzór P(A)+P(B')= 1− P(B)+ P(A∩ B) według was jest poprawny i drugie rozwiązanie zadania ?

sushi_ gg6397228: skąd masz wzór 2?

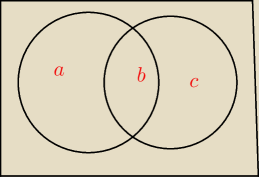
BlueJ: Narysowałam sobie w prostokącie ( całe zdarzenie) dwa koła jako zbiór A i B i zamalowałam P(A) i dopełnienie zbioru B, czyli P(B'). No stworzyłam taki wzór na podstawie moich graficznych wypocin No właśnie chciałabym się dowiedzieć czy zapisałam to poprawnie...

sushi_ gg6397228: P(A)+ P(B')= P(A)+ 1−P(B) ≠ P(AnB) + 1−P(B)

BlueJ: Czyli mój wzór nie jest prawdziwy, takk

sushi_ gg6397228: rozpisz sobie na literkach "a, "b", "c" , d− pole poza kołami" i sobie odpowiesz na pytanie