zadanie P@weł:

	π
Dla jakich wartośći parametru α∊(0;		) wielomian :
	2

W(x) = 2x³sin²α + x²sinαcosα − x − cos²α jest podzielny przez x−1 ? W(1) = 0 W(1) = 2sin²α + sinαcosα − 1 − cos²α = 0 2sin²α + sinαcosα − 1 − cos²α = 0 Pomoze ktos mi to dokonczyc Dalej nie umiem tego rozwiazc

Maslanek: 3sin²x+sinxcosx=0 sinx(3sinx+cosx)=0 sinx=0 lub 3sinx+cosx=0 itd. U mnie x=α z wygody pisania

P@weł: nie mam pojecia jak tobie to wyszlo , mi wychodzi inaczej: 2sin²α + sinαcosα − 1 − cos²α = 0 jak pod 1 podstawie : 1= sin²α + cos²α to mi wychodzi: 2sin²α + sinαcosα − sin²α − cos²α − cos²α = 0 sin²α + sinαcosα − 2cos²α MAslanek powiesz mi dokladnie jak to rozpisales?

Kaja: Maslanek ma źle. ty masz dobrze

P@weł: Kaju mozesz mi powiedziec jak to dalej rozpisac jestem noga z ttrygonometrii , te wszystkie cos sin mnie przytłaczaja

Kaja: sin²α+sinαcosα−cos²α−cos²α=0 sin²α−cos²α+sinαcosα−cos²α=0 (sinα−cosα)(sinα+cosα)+cosα(sinα−cosα)=0 (sinα−cosα)(sinα+cosα+cosα)=0

P@weł: no dobra ale co teraz z tym w nawiasie mam zrobic?

Kaja: sinx=cosx lub sinx+2cosx=0 masz może do tego zadania odpowiedzi?

P@weł: niestety nieee jedynie karte z zadaniami

P@weł: Kaju no dobra wyszlo takie rownania ale co z nimi zrobic

	1
gdyby wyszlo powiedzmy : sinx =
	2

to bym wieddzial co zrobic a z tym nieee...

ICSP: sinx = cosx v sinx + 2cosx = 0

	π
z pierwszego x =
	4

drugie :

	π
dla x ∊ (0 ;		) :
	2

0 < sinx + 2cosx zatem równanie sprzeczne.

	π
Ostatecznie x =
	4

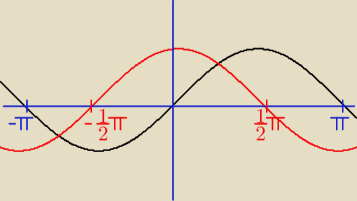
P@weł: ICSP dla pierwszej rownosci sinx=cosx o to chodzi co narysowalem na rysunku? mozesz jakos to skomentowac?

ICSP: Metoda graficzna, jak najbardziej poprawna.

P@weł:

	π
ICSP mozesz jeszcze mi powiedziec jak okresliles ze w pierwszym wyszlo x =		a dla
	4

	π
sinx + 2cosx = 0 ⇒ ( 0,		)
	2

ICSP: sinx − cosx = 0 √2 (U{√2]{2} sinx − U{√2]{2} cosx) = 0

	π		π
√2(sinx * cos		− cosx * sin		) = 0
	4		4

	π
√2sin(x −		) = 0
	4

	π
sin(x −		) = 0
	4

	π
x =
	4

P@weł: ICSP nie rozumiem, jak doprowadziles do tego ze z "sinx − cosx = 0 " nagle powstalo:

	√2		√2
√2(		sinx −		cosx )=0
	2		2

bardzo prosze o prostszy tok rozumowania

ICSP: Wyciągnąłem √2 przed nawias ? 2n + 4 = 2(n + 2) to samo

P@weł: tylko skad te √2 sie w ogole wzielo , Dobra zacznijmy jeszcze raz : W(x) = 2x³sin²α + x²sinαcosα − x − cos²α w(1) = 0 w(1)= 2sin²α + sinαcosα − 1 − cos²α= 1= sin²α + cos²α = 2sin²α + sinαcosα − sin²α − cos²α − cos²α= = sin²α + sinαcosα − cos²α − cos²α= = sin²α−cos²α+sinαcosα−cos²α=0 = (sinα−cosα)(sinα+cosα)+cosα(sinα−cosα)=0 = (sinα−cosα)(sinα+cosα+cosα)=0 sinx=cosx v sinx+2cosx=0 No i nie wiem jak te dwa równania wyżej rozpracowales ze wyszedl tobie jakis √2 i reszta, jestem slaby z tego , wiec prosze o wyrozumialosc, nie widze wszystkiego tak dobrze, musze to miec rozpracowane krok po kroku... Proszę o pomoc

ICSP: Drugie jest sprzeczne. Pierwsze : sinx = cosx Inny sposób :

	π
1o W przedziale (0 ;		) cosx jest różny od 0. Mogę zatem podzielić to równanie przez
	2

cosx i dostaje : tgx = 1

	π
x =
	4

P@weł:

	π
ICSP wlasnie o cos takiego mi chodzi teraz juz rozumiem skad to x =
	4

Tylko jeszcze mam 2 pytanka:

	π
1. Chodzi o to ze w tym przedziale (0;		) funkcja cosx nie przecina osi X
	2

	π
dlaczego akurat sprawdzamy dla przedziału (0;		)
	2

2. Z czego wynika ze drugie równanie jest sprzeczne Bardzo prosze o podpowiedź

ICSP: Przeczytałeś w ogóle polecenie ?

P@weł: ooo przepraszam faktycznie.... nie zwracalem na to uwagi podczas robienia zadania Czyli ze w tym przedziale funkcja cosx nie przecina osi x i moglbys wyjasnic jeszcze dlaczego sinx+2cosx=0 sprzeczne

ICSP: Znowu spójrz na przedział.

P@weł:

	π
dobra faktycznie w przedziale ( 0;		) funkcja cosx nie przecina osi X
	2

ale nadal nie rozumiem dlaczego sinα+2cosα=0 jest sprzeczne

ICSP:

	π
zbiory wartości funkcji sinx oraz cosx w przedziale (0 ;		) poproszę.
	2

P@weł: dla sinx ZW= <0,1> i dla cosx ZW= <0,1> chyba

ICSP:

	π
dla ( 0 ;		)
	2

P@weł: dla sinx ZW= (0,1) i dla cosx ZW= (0,1) na 100%

P@weł: ale jak to sie ma do tego ze sinα+2cosα=0 jest sprzeczne...

ICSP: sinx > 0 2cosx > 0 Dodająć stronami : sinx + 2cosx > 0 a jak jest > 0 to siłą rzeczy równe 0 być nie może. "Suma dwóch liczb dodatnich nie da 0"

P@weł: No i teraz wszystko wydaje sie byc o wiele bardziej zrozumiałe ! BARDZO DZIĘKUJĘ ISCP! dobrze ze sa na tym forum tak tęgie głowy jak ty