aa Hugo: A,B są zdarzeniami losowymi zawartymi w Ω wykaż że jeżeli P(A) = 0,9 i P(B) = 0,7 to P(AnB')≤3 wzór prawdziwy (AuB)=P(A)+P(B)−P(AnB) P(B)= 1−P(B') P(B')=0,3 (AuB')=P(A)+P(B')−P(AnB') (AuB')=0,9+0,3−P(AnB') (AuB') −1,2 =−P(AnB') 1,2−(AuB') =P(AnB') aby nierówność miała sens P(AnB')≤3, P(AuB') musi wynosić P(AuB') ≥ 0,9 a to jest zawsze spełnione gdyż sam samo prawdopodobieństwo P(A) = 0,9 Dobrze

Kaja: Hugo z ta treścią zadania chyba cos jest nie tak. tego nawet nie trzeba udowadnić, bo prawdopodobieństwo jest zawsze ≤ 1, więc tym na pewno ≤3. sprawdx treść

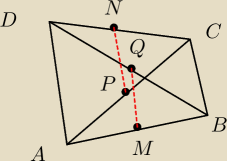
Hugo: Dany jest czworokąt wypukły ABCD niebędący równoległobokiem. Punkty M,N są odpowiednio środkami boków AB i CD. Punkty P, Q są odpowiednio środkami przekatnych AC i BD. Uzasadnij że MQ II PN. Jo ciekawe czy za rysunek dostane punkta... pewnie i tak źle

Hugo: Kajo : https://matematykaszkolna.pl/strona/3007.html Ale zawsze trzeba sie odnieść do tego wzoru uważam tak mnie uczyli

Hugo: Ale czy moje myślenie też jest dobre co do prawdopodobieństwa i wgl Wole po swojemu

Kaja: Hugo chodziło o treść. porównaj sobie , ze ty masz P(A∩B')≤3, a tam jest P(A∩B')≤0,3. a to juz jest różnica

Hugo: przemnożyłem x10 . . . . Bład zapisu.. na maturze bym pewnie sprawdził kilka razy dziś jednak chce zrobić jak najwiecej zadań .. a tak poza tym ok? .. mam nadzieje ! Tak głupio czegoś nie umieć bo matura w pon

Hugo: 80% mam bez tego zadania : >

Hugo: zrobila bys to zadanie ?

Kaja: nie przejmuj się tak bardzo

Hugo: czytam rozwiązanie i nie wychodzi albo inaczej: nie rozumiem https://matematykaszkolna.pl/strona/3005.html 80% to wynik zadowalający ale byle nie niżej

Hugo: 'Jeżeli w dowolnym trójkącie połączymy środki dowolnych dwóch boków, to powstały odcinek jest równoległy do trzeciego boku i jego długość jest równa połowie długości boku trzeciego.'

Hugo: Z tego twierdzenia wynika ze |QM| jest II do |DA| jak również |NP| II do |DA| ⇔ |NP| II |QM| tak może byc?

Hugo: .