matura
zawodus: Matura to bzdura 2
Zadanie 1 (5 pkt)
Rozwiąż nierówność
√1+2|x|+x2+2≥4|x+1|
Zadanie 2 (4 pkt)
Dany jest wielomian W(x)=x
5+5x
4+5x
3−5x
2−6x
Uzasadnij, że dla każdej liczby naturalnej n liczba W(n) jest podzielna przez 120.
Zadanie 3 (6 pkt)
Dla jakich wartości parametru k równanie x
4−(3k+2)x
2+k
2=0 ma rozwiązania, które są kolejnymi
wyrazami ciągu arytmetycznego?
Zadanie 4 (5 pkt)
Cztery liczby rzeczywiste tworzą ciąg geometryczny w których suma wyrazów skrajnych wynosi
−21,a pozostałych 6. Znajdź te liczby.
Zadanie 5 (4 pkt)
Z punktu A=(1,1) wychodzą dwie proste prostopadłe przecinające oś OX układu współrzędnych w
punktach B=(x
1,0) i C=(x
2,0), x
1,x
2≥0. Wykaż, że pole trójkąta ABC jest większe lub równe
1.
Zadanie 6 (3 pkt)
Uzasadnij, że dla a>0 i b>0 prawdziwa jest nierówność
Zadanie 7 (3 pkt)
Wyznacz najmniejszą i największą wartość funkcji
Zadanie 8 (4 pkt)
Oblicz prawdopodobieństwo tego, że 4 czterech rzutach symetryczną kostką do gry suma
wyrzuconych oczek będzie liczbą parzystą.
zadanie 9 (4 pkt)
Załoga złożona ze 175 robotników miała zbudować w określonym terminie odcinek autostrady A4. Po
30 dniach wspólnej pracy okazało się, że trzeba poprawić oddany wcześniej odcinek autostrady
A2. Dlatego codziennie zabierano do tego zadania kolejnych 3 robotników, wskutek czego
praceprzy budowie autostrady A4 zakończono z 21‑dniowym opóźnieniem. W jakim czasie planowano
pierwotnie wybudować dany odcinek autostrady A4?
Zadanie 10 (5 pkt)
Dany jest ostrosłup prawidłowy czworokątny. Odległości środka wysokości tego ostrosłupa od
krawędzi bocznej i od ściany bocznej wynoszą odpowiednio a i b. Oblicz objętość tego
ostrosłupa
Zadanie 11 (4 pkt)
W sześciokącie foremnym ABCDEF punkty M i N są odpowiednio środkami boków CD i DE. Odcinki AM i
MN przecinają się w punkcie P. Wykaż, że |<APB|=60
0.
Zadanie 12 (3 pkt)
Rozwiąż równanie
sin2x−2sinx=1−cosx
w przedziale <0,2π>
Powodzenia


3 maj 13:10
Marcin: 
3 maj 13:10
kyrtap: chyba tym razem będzie ciężej

3 maj 13:11
Beti: Zaczęłam ale się poddaje, setka na majowym mi nie potrzebna
3 maj 14:09
zombi: Za chwilę się biorę za to

3 maj 14:10
Saizou : zadanie 9 jakie życiowe

3 maj 14:13
Saizou : zad. 11 jest na pewno dobrze przepisane ?
3 maj 14:21
BeforeU: Odp w pierwszym? <−73, +∞) ?
3 maj 14:37
3 maj 14:39
BeforeU: to masz dobrze

3 maj 14:43
aaaa:(: oooooo zaraz zaczynam ciekawe czy coś zrobię

3 maj 14:43
zawodus: UWAGA
W 11 jest litrówka

Powinno być
odcinki AM i BN
Dzięki
Saizou 
3 maj 14:49
aaaa:(: w tym 1 rozbijając na 3 przypadki w każdym z nich musimy jeszcze potem uwzględnić po 2
przypadki prawda?
3 maj 15:03
BeforeU: Nie w tym pierwszym tylko 3 przypadki f(x) =x f(X) = x+1
3 maj 15:05
aaaa:(: dla przedziałów (−∞,−1)
<−1,0)
<0,+∞)
?
tylko jak sobie rozpisuję to potem nan pod pierwiastkiem albo (x+1)2 albo (x−1)2 a to jakby
kolejny moduł
3 maj 15:08
BeforeU: mozna pisać odpowiedzi?
3 maj 15:09
3 maj 15:11
BeforeU: czyli w sumie bedzie 6 przypadkow

3 maj 15:12
BeforeU: Zad 2.
(x−3)(x−2)(x−1)x(x+1) 5*4*3*2= 120
3 maj 15:13
Piotr 10: zad.6
Średnia arytmetyczna ≥ Średnia harmoniczna
3 maj 15:16
aaaa:(: no czyli 3 przypadki a w każdym z nich jeszcze po 2

zaraz obliczę i ogarnę czy mam tak samo

3 maj 15:17
BeforeU: Zad3. k∊ ( −∞ , −2 ) u (−25,+∞) prosze o sprawdzenie
3 maj 15:25
razor: po co sobie życie komplikować?
 √x2+2|x|+1
√x2+2|x|+1 =
√(|x|+1)2 = ||x|+1|
mamy więc
||x|+1| +2 ≥ 4|x+1|
3 maj 15:34
BeforeU: i tutaj zaczynaja sie komplikacje z opuszczniem tej wartosci bezwzglednej w dobrych
przedzialach dlatego preferuje wykres

3 maj 15:35
BeforeU: w 4 trzeba rozwiazac az taki dlugi uklad rownan czy jest jakis inny sposob?
3 maj 15:37
razor: wcale taki długi nie jest

za to chciałbym zobaczyć wasze rozwiązania zadania 11 bo zrobiłem
to sposobem tak okrężnym że chyba bardziej się nie dało

3 maj 15:39
52: Zad7.
| | 1 | |
Najmniejsza wartość funkcji to − |
| , a największa to 1 ? |
| | 3 | |
3 maj 15:46
razor: mam tak samo więc raczej tak
3 maj 15:50
aaaa:(: | | 7 | | 2 | |
w 1 mi wyszło x∊(− |
| , |
| ) czyli źle −.− |
| | 3 | | 5 | |
3 maj 15:50
52: Zad6
Jak się nie zna "średnich" to ostatnia postać po przekształceniu ? :
ab≠0
ab(a−b)
2≥0
oczywista oczywistość...
dobrze ?
3 maj 15:51
52: Dzięki razor
3 maj 15:51
muflon: (a−b)2≥0
3 maj 15:55
52: no właśnie nie jestem do końca przekonany czy to tak możemy zapisać w końcu to nierówność ..

3 maj 15:56
Piotr 10: Musisz dopisac komentarz jeszcze
3 maj 15:57
BeforeU: Zad 7 z czego trzeba skorzystac?
3 maj 16:09
muflon: z wiedzy, a raczej umiejętności

3 maj 16:10
Kanoniero: Ktoś robił 7 zadanie? Jak co to mi wyszło 23
3 maj 16:10
Kanoniero: to oczywiscie była wartość max
3 maj 16:12
muflon: jakimi rachunkami doszedłeś?
3 maj 16:23
Kanoniero: dobra cofam właśnie narysowałem sobie tego wykres i sie nie zgadza... probowalem wyznaczyc
wierzcholek paraboli w mianowniku i podstawic ale nic nie wyszlo dobrze
3 maj 16:26
Kanoniero: ktoś wie jak to zrobić?
3 maj 16:34
BeforeU: Probowalem tak samo z wierzcholkiem ale skąd mamy wiedziec gdzie jest max fucnkcji kwadratowej?
3 maj 16:39
muflon: Zawodus, a może zapomniałeś dopisać 2 przy x w mianowniku


3 maj 16:41
MCC: "BeforeU: Zad 2. (x−3)(x−2)(x−1)x(x+1) 5*4*3*2= 120"
moglby ktos wyjasnic mi zadanie 2,
rozumiem ze jest to wielomian W(x) rozlozony na czynniki to (x−3)(x−2)(x−1)x(x+1),
a 5*4*3*2= 120 jest z rozkladu 120 na czynniki pierwsze, ale czy ktos wyjasni mi zwiazek miedzy
jednym a drugim, poniewaz jesli mialbym taki dowod na maturze, to staralbym sie to tak
rozpisac aby wyciagnac 120 przed nawias.
3 maj 16:47
Kanoniero: z wykresu widać że to są 1 i −13
3 maj 16:47
BeforeU: jezeli masz 5 kolejnych liczb to jedna z nich ejst podzialna przez 5 jedna przez 4 jedna przez
3 jedna przez 2 jedna przez 1 . a iloczyn liczb podzielnych przez 1 ,2,3,4,5 jest
podzielny przez 120
3 maj 16:50
MCC: dzieki, teraz rozumiem

3 maj 16:54
BeforeU: Zad 8.
Na pewno "symetryczną" a nie sześcienna ?
3 maj 16:58
BeforeU: Zadane 8 2161296?
3 maj 17:15
Marcin:
| | x−1 | |
t= |
| ⇒ tx2+(t−1)x+t−1=0 |
| | x2+x+1 | |
Δ = (t−1)
2−4t(t−1)=0
Tak robiliście 7, czy jakoś inaczej?
3 maj 17:16
razor: Δ ≥ 0

ale koncept taki sam
3 maj 17:17
MCC: wg mnie oznacza to to samo,
czy dobrze rozwiazuje to zadanie?
ps. |Ω|=64
wylosowane liczby utworza ciag (a,b,c,d)
moga wypasc nastepujace przypadki (kolejnosc wypadniecia tych liczb nie ma znaczanie, tak?)
p−parzyste
n−nieprarzyste
(pppp)
(pppn)
(ppnn)
(pnnn)
(nnnn)
dwa z nich odrzucamy (2 i 4)
1)34=81
3)?
5)34=81
3 maj 17:18
Marcin: razor, według mnie dając Δ≥0, to liczysz zbiór wartości

3 maj 17:20
3 maj 17:20
razor: w sumie racja, ale na jedno wychodzi

3 maj 17:22
Marcin: No tak

Później policzę resztę

3 maj 17:23
BeforeU: p+p+p+n = to chyba nieparzysta bo np 2+2+2 +1 moze byc 2 parzyste labo 2 nieparzyte
lub 4 paryste lub 4 nieparzyste
p+p+p+p
n+n+n+n
p+n+p+n
p+p+n+n
czyli 4 przypadki liczb parzystych jest 3 i nieparzystych jest 3 czyli 3*3*3*3 = 81 −1
przypadek
4*81 = 324 Ω = 1296 A = 3241296
Tak to ma wygladac
3 maj 17:24
BeforeU: Dobrze zrobilem?
3 maj 17:27
razor:
PPPP − 3
4
NNNN − 3
4
|Ω| = 6
4
| | 8*34 | | 1 | | 1 | |
P(A) = |
| = 8* |
| 4 = |
| |
| | 64 | | 2 | | 2 | |
3 maj 17:30
MCC: wydaje mi sie ze dobrze dokonczyl moje rozwiazanie @razor
chodzi o to ze kolejnosc nie ma znaczenia, wiec przypadek ppnn i pnpn pokrywają się ( bo idac
tym tropem nalezaloby jeszcze zrobic przypadki: nnpp, pnnp, nppn npnp) i wtedy by sie
zagdazalo, poniewaz symbol newtona zastosowany przez razora pokazuje na ile sposobow mozemy
ulozyc ciag skladajacy sie z 2 parzystych i 2 nieparzystych liczb
3 maj 17:33
BeforeU: a wyjaśnisz skąd obliczyles to NNPP ?
3 maj 17:33
zombi: 4. liczby
(3,−6,12,−24) lub (−24,12,−6,3)
1. tak jak razorowi
2. iloczyn 5 kolejnych liczb n.
6. pomnożone am−gm
Resztę liczę.
3 maj 17:34
razor: | | | |
Wybierasz 2 miejsca dla liczb parzystych (lub nieparzystych, nie ma znaczenia) na | |
| | |
sposobów, miejsca liczb nieparzystych są już wtedy określone. Dalej liczby parzyste wybierasz
na 3*3 sposobów i nieparzyste też na 3*3 sposobów
3 maj 17:34
3 maj 17:37
Saizou : prawdopodobieństwo mozna też zrobić z drzewek xd
3 maj 17:39
Marcin: Ja się zawsze w te drzewka bawię

3 maj 17:39
zawodus: Jak wam idzie?

3 maj 17:40
Marcin: Ja nie robię, odpoczywam na razie

3 maj 17:41
Saizou : 4 poziomy to nie tak dużo, a tym bardziej że wylosowanie parzystej lub nieparzystej (za jednym
rzutem) jest równoprawdopodobne xd
3 maj 17:42
BeforeU: Czyli moge napisac przypadki ?
1)n+p+n+p
2)p+p+n+n
3)n+n+p+p czyli losuje 32 * 32 * 6 Nie jestem fanem
4)n+p+p+n wzorów w kombinatoryce
5)p+n+n+p
6)p+n+p+n
3 maj 17:42
MCC: | | | |
tak, to jest dokladnie to samo, bo | =3! liczy nam liczbe tych przypadkow, ktorych jest 6 |
| | |
3 maj 17:46
zombi: 5. ciekawe, ale nie wiem czy nie przekombinowałem

Wyszła ładna nierówność, więc mam
nadzieję, że jest poprawnie.
3 maj 17:47
zawodus: Ja myślałem, że napiszecie jedno zdanie i odpowiedź

Balem się, że dałem za łatwe, ale wy je
utrudniliście

3 maj 17:50
Saizou :
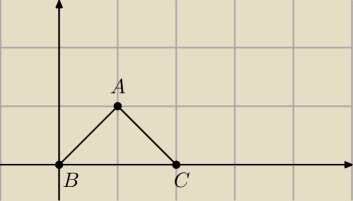
ważne żeby pokazać ze jeśli x
1<x
2 to
x
2−x
1≥2 i po zabawie xd
3 maj 17:55
zombi: Albo bez górnego założenia, że |x2−x2| ≥ 2
3 maj 18:00
aaaa:(: zad 6 wyszło mi: (a−b)
2≥0 dla a>0 i b>0 jest to >0. Wam też tak?

3 maj 18:02
Saizou : dokładnie tak jak piszesz xda na dodatek wiemy że ABC to trójką prostokątny

3 maj 18:02
zombi: Mi wyszło. Saizou zrób je do końca i powiedz mi do czego doszedłeś, bo mi ładnie powychodziło.
3 maj 18:03
Saizou :
skoro proste AB i AC są prostopadłe to przeciwprostokątna BC ΔABC jest najkrótsza dla
lABl=lACl=
√2, czyli wynosi ona 2 ⇒lx
1−x
2l≥2
2P
ABC=lx
1−x
2l⇒2P
ABC≥2⇒P
ABC≥1
3 maj 18:11
zombi: 

3 maj 18:15
zombi: Pole z wyznaczników czy tego wzoru z (xa−xb).. ?
3 maj 18:16
BeforeU: a skąd wiemy . że sa prostopadłe ? z rysunku ? Przeiz punkt B nie musi byc w 0.0
3 maj 18:16
Saizou : z treści zadanie

3 maj 18:16
Saizou :
| | 1 | |
zombi ze wzoru p= |
| ab  |
| | 2 | |
3 maj 18:17
Marcin: BeforeU

dwie proste
prostopadłe przecinające oś OX
3 maj 18:18
kyrtap: Mógłby ktoś przedstawić rozwiązanie algebraiczne zadania 1? bo graficznie wiem jak rozwiązać
3 maj 18:19
BeforeU: A no i znowu nie doczytałem tresci

3 maj 18:19
Marcin: ||x|+1| +2 ≥ 4|x+1|
kyrtap, z tym sobie nie poradzisz?

3 maj 18:21
kyrtap: co muszę najpierw z siatki znaków a potem z definicji ?
3 maj 18:23
Marcin: Ja liczyłbym tak
|x|+1 ≥ 4|x+1| −2
|x|+1 ≤ −(4|x+1| −2)
i suma zbiorów.
3 maj 18:26
Piotr 10: Możecie podać odpowiedz do zadania z ostroslupem, bo zaraz ide z kompa

?
3 maj 18:27
ICSP: a ja bym zapomniał o zewnętrznej wartości bezwzględnej.
3 maj 18:28
jakubs: |x|+1≥4|x+1|+2
|x|+1≤−4|x+1|−2
I co teraz na przedziały ?
3 maj 18:29
zawodus: Jakoś nikt nie ruszył jeszcze 3,9,10 11 12

Czekamy

3 maj 18:29
Piotr 10: zawodus mozesz podac odpowiedz do zad z ostroslupem? Bo zaraz musze isc i na kompa nie
bede mogl wbic, a pozniej bym sobie zrobil
3 maj 18:30
Marcin:
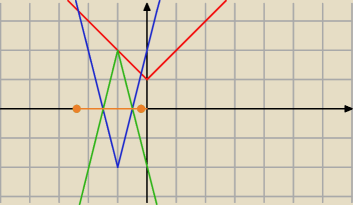
Graficznie nie jest tak kolorowo, bo ciezko cokolwiek odczytać

3 maj 18:31
zawodus: Może jutro?

Bo jak dam odpowiedz to będziecie liczyć pod nią

Wiem, bo tak sam często robię

3 maj 18:33
Piotr 10: Hehe

ok
3 maj 18:33
zombi: Ja zrobiłem 12.
3 maj 18:34
Marcin: 12 takie typowe jest

3 maj 18:35
zombi: Z ostrosłupem trzeba wykorzystać trójkąty podobne, tylko wyniki jakieś gówniane mi wychodzą.
3 maj 18:38
zawodus: No 12 było najłatwiejsze

3 maj 18:40
zombi: zawodus a mógłbyś podać odpowiedź do ostrosłupa?
3 maj 18:41
kyrtap: Jeżeli doprowadziłem wielomian W(n) = n(n−1)(n+1)(n+2)(n+3) + komentarz mój jest poprawnie?
3 maj 18:43
Piotr 10: Tak
3 maj 18:44
Marcin: Zależy co to za komentarz

3 maj 18:44
zawodus: zombi wynik nie jest najpiękniejszy, ale to mają do siebie zadania, w których nie ma
danych liczbowych

3 maj 18:44
Piotr 10: Komentarz − ''A dalej to oczywista oczywistość''

3 maj 18:44
kyrtap: Marcin na pewno mądry komentarz

3 maj 18:44
MCC: czy w zadaniu 3 jest dobra tresc, chodzi o to, czy w tresci zadanio pominiete to, ile powinno
byc rozwiazan?
3 maj 18:45
zawodus: Czy każdy chce znać odpowiedź do ostrosłupa?

żeby nie było, że reszta nie będzie robić jak
go zobaczy

3 maj 18:45
Piotr 10: Nie gadaj głupot, dawaj odpowiedź

3 maj 18:46
MCC: "BeforeU: Zad3. k∊ ( −∞ , −2 ) u (−25,+∞) prosze o sprawdzenie"
czy to jest dobrze?
3 maj 18:47
kyrtap: ja nie chcę np zawodus

3 maj 18:47
razor: Ja się właśnie zorientowałem że źle przeczytałem polecenie więc robię jeszcze raz

3 maj 18:47
Marcin: No podaj, bo Piotrek psychicznie nie wytrzyma

3 maj 18:48
MCC: niewazne, ta odpowiedz jest troche bez sensu
3 maj 18:48
Marcin: No faktycznie dziwna odpowiedz

3 maj 18:49
razor: zrobiłem

ale wynik ładnie nie wygląda
3 maj 19:00
zombi: U mnie też
3 maj 19:03
bans: we wtorek maturka szykujcie koszule, krawwaty długopisy i JEDZIEMY Z TYM KOKSEM !
3 maj 19:08
MCC: ponawiam pytanie o zad 3, czy w tresci nie ma podanej liczby rozwiazan?
3 maj 19:08
muflon: a no koszula poszła się prać

3 maj 19:12
BeforeU: MCC to zrob i przedstaw swoje rozwiazanie
3 maj 19:14
kyrtap: w zadaniu z ciągiem 2 serie rozwiązań?
3 maj 19:14
kyrtap: | | −21 | |
i mam pytanie jeżeli wyznaczę a1 = |
| i podstawię do drugiego równania to jeżeli mam |
| | 1+q3 | |
1 + q
3 w mianowniku i potem wyjdzie q = −1 to nie biorę tego tak bo q nie należy do
dziedziny, wiem że niby to proste ale pytam się tak na zaś

3 maj 19:17
razor: musisz napisać uzasadnienie co się dzieje jak q = −1 bo zauważ że dzieliłbyś wtedy przez 0
3 maj 19:18
kyrtap: no napisałem że nie należy do dziedziny
3 maj 19:18
razor: tak, ale na jakiej podstawie ustaliłeś tę dziedzinę? Musisz podstawić q = −1 do pierwotnego
równania i napisać, że wtedy wychodzą bzdury więc q ≠ −1
3 maj 19:19
kyrtap: no ale jeżeli w mianowniku jest to to chyba jasne że mianownik musi być różny od zera więc ten
wynik wyrzucam
3 maj 19:21
MCC: ( −∞ , −2 ) u (−25,+∞)
to rozwiazanie jest dziwne bo gdy je zsumujesz x∊R,znaczy to jest mozliwe (malo prawdopodobne
ale mozliwe) ale chodzi o to, ze nie umiem tego zrobic, bo skoro ma byc ciag, to chyba powinny
byc przynajmniej trzy rozwiazania, a ich ilosc jest nieograniczona
3 maj 19:22
Marcin:
a+aq
3=−21
| | 6 | |
aq+aq2=6 ⇒ a(q+q2)=6 ⇒ a= |
| |
| | q+q2 | |
| 6 | | 6 | |
| + |
| *q3=−21 → q+q2≠0 → q(1+q)≠0 → q≠−1, q≠0 |
| q+q2 | | q+q2 | |
6+6q
3=−21q−21q
2
Tak, mają być dwa rozwiązania według mnie

3 maj 19:24
razor: nie możecie sobie tak po prostu podzielić bez żadnego uzasadnienia

na maturze obcinają za to
punkty. Trzeba zobaczyć co się dzieje gdy mianownik się zeruje, i napisać uzasadnienie
3 maj 19:26
Marcin: MCC to weź wstaw sobie losową liczbę z Twojego rozwiązania i zobacz czy pierwiastki utworzą
ciąg arytmetyczny

3 maj 19:26
Marcin: Napisałem dziedzinę, tylko troszkę później

3 maj 19:27
kyrtap: moim zdaniem tak jak Marcin jest dobrze zawsze tak robiłem i Pani nie ucinała punktów
3 maj 19:28
Marcin: Ja bym tylko napisał, ze q≠−1 i q≠0. W sumie to się nie zastanawiałem nad tym, czy odjęliby za
to punkty

3 maj 19:33
muflon: zadanie 5:
Sposób Saizou bardzo dobry

Mój trochę dłuższy
Zauważam, że te trójkąty mają stałą wysokość 1
Więc najmniejsze pole będzie dla najmniejszej podstawy
oznaczam obie proste:
y=ax+b
y=−1/a+c
Wyznaczam b i c podstawiając A(1;1)
wyliczam miejsca zerowe x
1 i x
2 z wzoru if: y=ax+b x
0=−b/a
Podstawa to będzie Ix
2−x
1I w module będę miał funkcje kwadratową, wyznaczam wierzchołek
paraboli i liczę że minimalna podatwa to będzie 2.
Wtedy Pole minimalne trójkąta to 2*1/2=1
P trójkąta≥1
c.n.u
3 maj 19:35
kyrtap: proszę o wypowiedzenie się ekspertów w tej sprawie odnośnie warunków

3 maj 19:36
3 maj 19:37
kyrtap: Marcin wejdziesz na gmaila?
3 maj 19:38
Marcin: Pewnie, już jestem

3 maj 19:39
zawodus: MCC odpowiedzi poprawne.


3 maj 19:47
kyrtap: zawodus wypowiesz się na temat ciągu?
3 maj 19:49
Marcin: Powiedz mi jeszcze jak zrobiłeś to 3 zadanie, bo ja jakoś nie mam pomysłu.
3 maj 19:49
Saizou :
zacznij od postaci iloczynowej xd
3 maj 19:52
zawodus: A jakie proponujecie rozwiązania w drugim?
3 maj 19:53
Saizou : ja już podałem swoją opcje

3 maj 19:54
Marcin: 4 to mozolne rozbrajanie wielomianu

Saizou, ale że jak?

3 maj 19:55
zawodus: Źle spojrzałem

Drugie jest już rozwiązane

3 maj 19:55
Marcin: 2*!

3 maj 19:55
Saizou :
tylko mnie intryguje stwierdzenie że ma rozwiązania, które są kolejnymi wyrazami ciągu ayt.
ile tych rozwiązań ma

3 maj 19:55
zawodus: wskazówka do 3
Trzeba rozważyć dwa przypadki
3 rozwiązania lub
4 rozwiązania

Dla mnie 3 rozwiązania = 3 rożne rozwiązania
4 rozwiązania = 4 różne rozwiązania

3 maj 20:02
Saizou : tak też myślałem

3 maj 20:07
MCC: troche sie spialem, ale osobiscie uwazam ze czego takiego na maturze nie bedzie, nie oszukujmy
sie, jest za trudne
skoro musimy miec ciag, wiec musza byc co najmniej 3 rozwiazania
te trzy pierwiastki to a1 − r < a1 < a1 + r . wiec mamy uklad
| ⎧ | (a−r)4−(3k+2)(a−r)2+k2=0 | |
| ⎨ | a4−(3k+2)a2+k2=0 |
|
| ⎩ | (a+r)4−(3k+2)(a+r)2+k2=0 | |
3 maj 20:08
razor: a co gdy ma 2 rozwiązania? 2 liczby zawsze tworzą ciąg arytmetyczny więc też chyba się powinno
wliczać?
3 maj 20:09
kyrtap: razor trzy liczby tworzą ciąg
3 maj 20:11
kyrtap: lub więcej
3 maj 20:11
MCC: wydaje mi sie ze po prostu tresc zadania jest zla, znaczy brakuje w niej, dla ilu rozwiazan
(powinno byc ze 3 lub wiecej)
3 maj 20:12
zawodus: razor tutaj do końca nie wiem jak jest, np Pan Andrzej Kiełbasa podaje, że ciąg aby był
arytmetyczny lub geometryczny musi posiadać co najmniej 3 wyrazy. Moja książka (rok 1992) też
tak podaje.
Nie zastanawiałem się nad tym

Podpytamy "starszych"

3 maj 20:15
MCC: znalazlem teraz to samo rownanie, ale z inna trescia zadania w necie, (3 lub wiecej) jest
rozwiazane na 2 sposoby, ale nie wiem czy moge podawac tutaj link do zewnetrznych stron
3 maj 20:17
zawodus: MCC możesz zawsze przepisać

3 maj 20:19
zawodus: Proponuję poprawić treść zadania na:
Dla jakich wartości parametru k równanie x
4−(3k+2)x
2+k
2=0 ma
co najmniej trzy różne
rozwiązania, które są kolejnymi wyrazami ciągu arytmetycznego?
Teraz nie będzie wątpliwości

3 maj 20:23
zawodus: Widzę, że maturka was przerosła

3 maj 21:19
razor: wrzucisz rozwiązanie zadania 9, albo chociaż jakąś wskazówkę? próbowałem robić ale wychodziły
mi jakieś bzdury
3 maj 21:35
MCC: 2 sposob jest taki, ze za x
2 podstawiamy t
t
2 − (3k+ 2)t+ k
2 = 0 .
zeby rownanie mialo 4 rozwiazanie, nasze rownanie z te musi miec 2 rozwiazania dodatnie t
1 i
t
2,
wtedy rozwiazaniami orginalne rownania są ±
√t1 i ±
√t2,
wtedy nasz ciąg możemy ułożyć na 4 rozne sposoby
jakiej liczby tworzą ciąg arytmetyczny.
(−
√t2,−
√t1,
√t1)
(−
√t1,−
√t2,
√t1)
(−
√t1,
√t2,
√t1)
(−
√t1,
√t1,
√t2).
korzystajac z wlasnosci ciagu arytmetycznego 2b=a+c
−2
√t1=−
√t2+
√t1 ⇒ 3
√t1=
√t2 ⇒ t
2=9t
1
−2
√t2=−
√t1+
√t1⇒ t
2=0
2
√t2=−
√t1+
√t1⇒ t
2=0
2
√t1=−
√t1+
√t2⇒ 3
√t1=
√t2 ⇒ t
2=9t
1
wrocmy do rownania i sprawdzmy co sie dzieje gdy t=0
t
2 − (3k+ 2)t+ k
2 = 0 ⇒ k
2=0 ⇒k=0
nasze rownanie ma wtedy postac t
2−2t=0 ⇒ t(t−2)=0 ⇒ x
2(x
2−2)=0 ⇒x
2(x−
√2)(x+
√2)=0
x
1=0 v x
2=
√2 v x
3=−
√2
(−
√2,0,
√2)− c.arytmetyczny, k∊do rozwiazania
pozostalo sprawdzic dla jakich wartosci k, nasze rownanie z "t" ma 2 dodatnie rozwizania,
spelniajace warunek t
2=9t
1
−b+
√Δ=9(−b−
√Δ) ⇒ 10
√Δ=−8b ⇒ 5
√Δ=−4b |( )
2 ⇒
⇒25Δ=16b
2 ⇒ 25(b
2−4ac)=16b
2 ⇒ 9b
2−100ac=0
i teraz z dane z rownania
3
2*(3k+2)
2 −100k
2=0 ⇒(9k+6)
2−(10k)
2=0
(9k+6−10k)(9k+6+10k)=0
(6−k)(19k+6)=0
| | 6 | |
k=6 v k=− |
| v (z poprzednieg przypadku) k=0 |
| | 19 | |
Otrzymane wartości k trzeba sprawdzić – po drodze równanie podnosiliśmy do kwadratu, więc mogły
się pojawić jakieś fałszywe rozwiązania.
(mozna po prostu podstawic k do rownania i zobaczyc czy otrzymane pierwiastki tworza ciag
arytmetyczmy), ale tez mozemy przeprowadzic analize przekształceń
Był tylko jeden taki moment, gdy podnosiliśmy równanie do kwadratu
5
√Δ=−4b |( )
2
25Δ=16b
2
Kiedy to przejście jest równoważnością (tzn. nie dokładamy żadnych dodatkowych pierwiastków)? –
jeżeli wiemy, że obie strony są dodatnie. Lewa jest, a prawa jest, o ile b < 0 – tak jednak
| | 6 | |
jest zarówno dla k=6 i dla k=− |
| |
| | 19 | |
3 maj 21:39
Marcin: Zdecydowanie niematuralne zadanie.

3 maj 21:41
MCC: tez tak sadze, zawodus chyba troszke przeszadzil
3 maj 21:45
razor: to co z tym zadaniem 9 zawodus?

3 maj 23:02
zawodus: Zadanie 9 jest z poziomu podstawowego

Tamto rzeczywiście trochę za trudne

Ale jak wam daję łatwe, to 10 minut i po sprawie

4 maj 09:28
Marcin: Musimy załozyć, że każdy pracownik pracuje z tą samą wydajnością, czyli zadanie traci swój
realizm

4 maj 10:12
Saizou : Marcin zadanie traci swój realizm, bo 174 pracowników się przygląda a tylko 1 robi

4 maj 10:30
Marcin: Tak bym napisał na maturze

4 maj 10:31
zawodus: To w Polsce tak tylko

Każde zagadnienie rzeczywiste w teorii jest i realizowane

4 maj 10:39
zawodus: Marcin egzaminator napisał by, 1 pkt /5 za inteligencję

4 maj 10:41
Marcin: Jak dla mnie, to powinni dać maxa

4 maj 10:54
Domel: Czy zapis
Dlatego codziennie zabierano do tego zadania kolejnych 3 robotników oznacza,
że 1−go dnia na A2 zabrano 3 prac. 2−go dnia 6 prac, 3−go dnia − 9 prac. czy może, że 1−go dnia
wzięto 3 pracowników, po pracy ich odwieziono na A4 a 2−go dnia wzięto 3 kolejnych wypoczętych

i tak każdego dnia

4 maj 10:58
zombi: Zadanie z podstawy tylko dlatego, że nie wymaga użycia narzędzi z rozszerzenia. Samo
stwierdzenie, że pochodzi z podstawy nie umniejsza trudności tego zadania. Wiele było takich
zadanek, które pochodziły z podstawy a zaginały wielu rozszerzonych. Moim zdaniem
szufladkowanie podstawa/rozszerzenie wcale nie oddaje realnej trudności zadania, jednak w
większości przypadków R oznacza trudniejsze.
4 maj 10:58
Domel: It's a joke

4 maj 11:06
Matejko: zawodus podaj odpowiedzi do wszystkich bez rozwiązań same odpowiedzi
4 maj 11:09
zawodus: Domel codziennie zabierano po 3 robotników

W sumie pierwszego dnia zabrano 3, po dwóch dniach na budowie było o 6 mniej itd.
Za chwilę podań odpowiedzi do zadań, które nie są dowodami

4 maj 11:49
Domel: No cóż − to mamy "problem".....

z ciągiem..................... arytmetycznym − a właściwie
− to będzie potrzebna suma ciągu
4 maj 12:01
zawodus: Oficjalne odpowiedzi:
Zadanie 1
Zadanie 2
dowód
Zadanie 3
Zadanie 4
te liczby to:
−24,12,−6, 3 i tworzą dwa ciągi
 Zadanie 5
Zadanie 5
dowód
Zadanie 6
dowód
Zadanie 7
Zadanie 8
Zadanie 9
Pierwotnie prace miały trwać 58 dni
Zadanie 10
| | 16a3b3 | |
V= |
| , 0<b<a<b√2 |
| | 3(a2−b2)√2b2−a2 | |
Zadanie 11
dowód
Zadanie 12
Jak macie uwagi to czekam

mogły się trafić pomyłki w przepisywaniu

4 maj 12:36
oskar: W tym z pracą będzie suma ciągu aryt.
Myślałem nad czymś takim
Niech t − czas potrzebny, aby ukończyć w terminie wobec tego całkowita praca to
175*t
natomiast nasi robotnicy robią to tak:
30*175 + 172*(a−30+1) + 169(a−30+2) + ... + 112(a−30+21) = 175a tylko nie wiem czy wyjdzie z
tego coś.
4 maj 14:14
zawodus: A co oznacza a?
Pomysł nawet niezły

4 maj 14:21
oskar: a mialo byc t

4 maj 14:25
zawodus: Problem w tym że prace wydłużyły się o 21 dni stosunku do zaplanowanego planu a nie do 30 dni

4 maj 14:31
MCC: zawodus− czy aby napewno 58? wyszlo mi 47,7≈48
4 maj 15:36
MCC: teraz mam wrazenie ze pominąlem cos istotnego w zadaniu, i przez co zle zrobilem zadanie
4 maj 16:10
zawodus: MCC pokaż rachunki

4 maj 19:46
Domel: zawodus − tak można

d − ilość dni do planowego zakończenia prac na A4 (od 30 dnia)
n − ilość dni do faktycznego zakończenia prac − n = d + 21
1. Obliczam ile osobodni poświęcono na naprawę A2
| | 1+n | |
T1 = 3+6+9+...+3n = 3*(1+2+3+...+n) = 3*( |
| *n) |
| | 2 | |
2. Obliczam stratę osobodni z powodu napraw A2
T
2 = 175* 21 = 3675
| | 1+n | |
T1 = T2 => 3* |
| *n = 3675 |
| | 2 | |
n
2 + n − 2450 = 0
Δ = 1 + 9800 = 9801 =>
√Δ = 99
| | −1−99 | |
n1 = |
| = −50 −> odpada |
| | 2 | |
d = n−21 = 49−21 = 28
D = 30 + d = 30 + 28 = 58
A może ktoś inaczej to zrobi ?

5 maj 00:42
mietek: Domel elegancko

tylko zwrot "osobodni" bym zamienił na roboczodniówki

Ja liczyłem przy pomocy równania, ale rachunki identyczne

5 maj 08:22
lisek: bzdura mietek ty nic nie umiesz tylko obrażasz innych

5 maj 08:40
mietek: umiem więcej niż ty

5 maj 08:42
lisek: Ja mam 3 doktoraty !
5 maj 08:43
mietek: drogie były? w ogóle to po co ja z tobą rozmawiam? szkoda mojego czasu na ciebie...
5 maj 08:47
daras: panowie ja mam doktorat honoriscausa uniwersytetu w Wollongong

5 maj 09:24
zawodus: Widzę, że jakieś zamieszki tutaj były

Rozwiązanie
Domela poprawne

5 maj 10:23
Domel: Ale mnie nie przebijecie − pisałem rozprawkę na temat wpływu zorzy polarnej na rozwój kolarstwa
w Chinach

A poważnie + próbowałem też zad. 9 robić za pomocą pojedynczego równania i liczyłem, że ktoś to
podejmie. Ale z braku odzewu − to chyba też poprawnie
L − droga na A4 do zrobienia od 30 dnia
d − ilość dni do planowego zakończenia prac na A4 (od 30 dnia)
n − ilość dni do faktycznego zakończenia prac − n = d + 21
L = 175*d = 175*(n−21) = 175n − 3675
A drugie równanie zakłada pracę pewnej liczby pracowników przez 1 dzień
L = (175−3)*1 + (175−6)*1 + (175−9)*1 + ... + [175−(3n−3)]*1 + (175−3n)*1
L = (175−3) + (175−6) + (175−9) + ... + [175−(3n−3)] + (175−3n)
| | 1+n | |
L = 175*n − (3+6+9+...+n) = 175n − 3(1+2+3+...+n) = 175n − 3*( |
| *n) |
| | 2 | |
| | 1+n | |
175n − 3*( |
| *n) = 175n − 3675 |
| | 2 | |
n
2 + n − 2450 = 0
No a dalej to jak w moim poście z godz. 00:42
5 maj 10:55
zawodus: Ja liczyłem jakoś tak
t− liczba dni planowa
t−30+21=t−9 − liczba dni, gdzie ubywało pracowników
175t − praca do wykonania
Mamy ciąg arytmetyczny a
n=175−3n
| | 172+175−3*(t−9) | |
St−9= |
| *(t−9) |
| | 2 | |
Dostajemy równanie
| | 172+175−3*(t−9) | |
175t=175*30+ |
| *(t−9) |
| | 2 | |
rozwiązanie to t=58

5 maj 11:27
Bogdan:
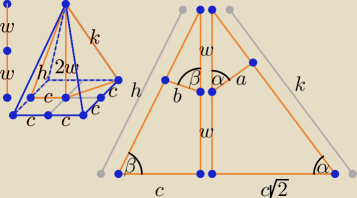
Szkic rozwiązania, może komuś się przyda.
h
2 = 4w
2 + c
2 k
2 = 4w
2 + 2c
2
| | b2 | | c2 | | a2 | | 2c2 | |
cos2β = |
| = |
| cos2α = |
| = |
| |
| | w2 | | h2 | | w2 | | k2 | |
c
2 w
2 = b
2(4w
2 + c
2) a
2(4w
a + 2c
2) = 2c
2w
2 ⇒ 2a
2w
2 = c
2(w
2 − a
2)
| | 4b2w2 | | 4b2w2 | |
c2 = |
| 2a2w2 = |
| *(w2 − a2) |
| | w2 − b2 | | w2 − b2 | |
| | 2a2b2 | |
c2w2 − b2c2 = 4b2w2 ⇒ c2 = |
| |
| | a2 − b2 | |
| | 1 | | 1 | | 2a2b2 | | ab | |
Objętość V = |
| *4c2*2w = |
| *4* |
| *2* |
| = ... |
| | 3 | | 3 | | a2 − b2 | | √2b2 − a2 | |
5 maj 17:07
Bogdan:
Chodzi o rozwiązanie zadania 10. Nie widzę swojego rysunku dołączonego do tego
rozwiązania.
5 maj 17:12
Baysonn: Na czym polega mój błąd w rozumowaniu w rozwiązywaniu zadania 9?
T− termin planowany zakończenia prac.
175T=W
175*30+[175−3(T+21)](T+21)=W
6 maj 22:51
Matejko: zaraz zrobie
8 maj 14:52








 Powinno być odcinki AM i BN
Dzięki Saizou
Powinno być odcinki AM i BN
Dzięki Saizou 

 zaraz obliczę i ogarnę czy mam tak samo
zaraz obliczę i ogarnę czy mam tak samo

 √x2+2|x|+1 = √(|x|+1)2 = ||x|+1|
mamy więc
||x|+1| +2 ≥ 4|x+1|
√x2+2|x|+1 = √(|x|+1)2 = ||x|+1|
mamy więc
||x|+1| +2 ≥ 4|x+1|

 za to chciałbym zobaczyć wasze rozwiązania zadania 11 bo zrobiłem
to sposobem tak okrężnym że chyba bardziej się nie dało
za to chciałbym zobaczyć wasze rozwiązania zadania 11 bo zrobiłem
to sposobem tak okrężnym że chyba bardziej się nie dało 





 ale koncept taki sam
ale koncept taki sam


 Później policzę resztę
Później policzę resztę 



 Wyszła ładna nierówność, więc mam
nadzieję, że jest poprawnie.
Wyszła ładna nierówność, więc mam
nadzieję, że jest poprawnie.
 Balem się, że dałem za łatwe, ale wy je
utrudniliście
Balem się, że dałem za łatwe, ale wy je
utrudniliście 
 ważne żeby pokazać ze jeśli x1<x2 to
x2−x1≥2 i po zabawie xd
ważne żeby pokazać ze jeśli x1<x2 to
x2−x1≥2 i po zabawie xd






 dwie proste prostopadłe przecinające oś OX
dwie proste prostopadłe przecinające oś OX


 ?
?
 Czekamy
Czekamy 
 Graficznie nie jest tak kolorowo, bo ciezko cokolwiek odczytać
Graficznie nie jest tak kolorowo, bo ciezko cokolwiek odczytać 
 Bo jak dam odpowiedz to będziecie liczyć pod nią
Bo jak dam odpowiedz to będziecie liczyć pod nią  Wiem, bo tak sam często robię
Wiem, bo tak sam często robię 
 ok
ok






 żeby nie było, że reszta nie będzie robić jak
go zobaczy
żeby nie było, że reszta nie będzie robić jak
go zobaczy 





 ale wynik ładnie nie wygląda
ale wynik ładnie nie wygląda



 na maturze obcinają za to
punkty. Trzeba zobaczyć co się dzieje gdy mianownik się zeruje, i napisać uzasadnienie
na maturze obcinają za to
punkty. Trzeba zobaczyć co się dzieje gdy mianownik się zeruje, i napisać uzasadnienie



 Mój trochę dłuższy
Zauważam, że te trójkąty mają stałą wysokość 1
Więc najmniejsze pole będzie dla najmniejszej podstawy
oznaczam obie proste:
y=ax+b
y=−1/a+c
Wyznaczam b i c podstawiając A(1;1)
wyliczam miejsca zerowe x1 i x2 z wzoru if: y=ax+b x0=−b/a
Podstawa to będzie Ix2−x1I w module będę miał funkcje kwadratową, wyznaczam wierzchołek
paraboli i liczę że minimalna podatwa to będzie 2.
Wtedy Pole minimalne trójkąta to 2*1/2=1
P trójkąta≥1
c.n.u
Mój trochę dłuższy
Zauważam, że te trójkąty mają stałą wysokość 1
Więc najmniejsze pole będzie dla najmniejszej podstawy
oznaczam obie proste:
y=ax+b
y=−1/a+c
Wyznaczam b i c podstawiając A(1;1)
wyliczam miejsca zerowe x1 i x2 z wzoru if: y=ax+b x0=−b/a
Podstawa to będzie Ix2−x1I w module będę miał funkcje kwadratową, wyznaczam wierzchołek
paraboli i liczę że minimalna podatwa to będzie 2.
Wtedy Pole minimalne trójkąta to 2*1/2=1
P trójkąta≥1
c.n.u





 Saizou, ale że jak?
Saizou, ale że jak? 
 Drugie jest już rozwiązane
Drugie jest już rozwiązane 


 Dla mnie 3 rozwiązania = 3 rożne rozwiązania
4 rozwiązania = 4 różne rozwiązania
Dla mnie 3 rozwiązania = 3 rożne rozwiązania
4 rozwiązania = 4 różne rozwiązania


 Podpytamy "starszych"
Podpytamy "starszych" 





 Tamto rzeczywiście trochę za trudne
Tamto rzeczywiście trochę za trudne  Ale jak wam daję łatwe, to 10 minut i po sprawie
Ale jak wam daję łatwe, to 10 minut i po sprawie 



 Każde zagadnienie rzeczywiste w teorii jest i realizowane
Każde zagadnienie rzeczywiste w teorii jest i realizowane 


 i tak każdego dnia
i tak każdego dnia 

 W sumie pierwszego dnia zabrano 3, po dwóch dniach na budowie było o 6 mniej itd.
Za chwilę podań odpowiedzi do zadań, które nie są dowodami
W sumie pierwszego dnia zabrano 3, po dwóch dniach na budowie było o 6 mniej itd.
Za chwilę podań odpowiedzi do zadań, które nie są dowodami 
 z ciągiem..................... arytmetycznym − a właściwie
− to będzie potrzebna suma ciągu
z ciągiem..................... arytmetycznym − a właściwie
− to będzie potrzebna suma ciągu
 Zadanie 5
dowód
Zadanie 6
dowód
Zadanie 7
Zadanie 5
dowód
Zadanie 6
dowód
Zadanie 7
 mogły się trafić pomyłki w przepisywaniu
mogły się trafić pomyłki w przepisywaniu 




 d − ilość dni do planowego zakończenia prac na A4 (od 30 dnia)
n − ilość dni do faktycznego zakończenia prac − n = d + 21
1. Obliczam ile osobodni poświęcono na naprawę A2
d − ilość dni do planowego zakończenia prac na A4 (od 30 dnia)
n − ilość dni do faktycznego zakończenia prac − n = d + 21
1. Obliczam ile osobodni poświęcono na naprawę A2

 tylko zwrot "osobodni" bym zamienił na roboczodniówki
tylko zwrot "osobodni" bym zamienił na roboczodniówki  Ja liczyłem przy pomocy równania, ale rachunki identyczne
Ja liczyłem przy pomocy równania, ale rachunki identyczne 



 Rozwiązanie Domela poprawne
Rozwiązanie Domela poprawne 
 A poważnie + próbowałem też zad. 9 robić za pomocą pojedynczego równania i liczyłem, że ktoś to
podejmie. Ale z braku odzewu − to chyba też poprawnie
L − droga na A4 do zrobienia od 30 dnia
d − ilość dni do planowego zakończenia prac na A4 (od 30 dnia)
n − ilość dni do faktycznego zakończenia prac − n = d + 21
L = 175*d = 175*(n−21) = 175n − 3675
A drugie równanie zakłada pracę pewnej liczby pracowników przez 1 dzień
L = (175−3)*1 + (175−6)*1 + (175−9)*1 + ... + [175−(3n−3)]*1 + (175−3n)*1
L = (175−3) + (175−6) + (175−9) + ... + [175−(3n−3)] + (175−3n)
A poważnie + próbowałem też zad. 9 robić za pomocą pojedynczego równania i liczyłem, że ktoś to
podejmie. Ale z braku odzewu − to chyba też poprawnie
L − droga na A4 do zrobienia od 30 dnia
d − ilość dni do planowego zakończenia prac na A4 (od 30 dnia)
n − ilość dni do faktycznego zakończenia prac − n = d + 21
L = 175*d = 175*(n−21) = 175n − 3675
A drugie równanie zakłada pracę pewnej liczby pracowników przez 1 dzień
L = (175−3)*1 + (175−6)*1 + (175−9)*1 + ... + [175−(3n−3)]*1 + (175−3n)*1
L = (175−3) + (175−6) + (175−9) + ... + [175−(3n−3)] + (175−3n)

 Szkic rozwiązania, może komuś się przyda.
h2 = 4w2 + c2 k2 = 4w2 + 2c2
Szkic rozwiązania, może komuś się przyda.
h2 = 4w2 + c2 k2 = 4w2 + 2c2