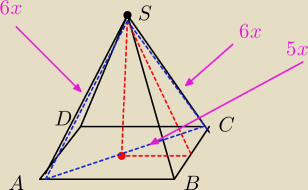
aa Hugo: Dany jest ostrosłup prawidłowy czworokątny ABCDS o podstawie ABCD. W trójkącie równoramiennym ASC stosunek podstawy do długości ramienia jest równy |AC|AS|=6:5 Oblicz sinus kata nachylenia ściany bocznej do płaszczyzny podstawy.

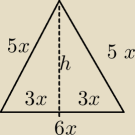Hugo: TAM MAM ŹLE W TYM RYSUNKU PODSTAWA MA 5 x z tw. pitagorasa: 25x² = h² + 9x² h=4x Następnie liczymy długość podstawy krawędzi, podstawa to kwadrat zatem przekątna to a√2 podstawy: 6x=a√2

	6x√2
a=
	2

Hugo: ... znaczy 6 x ma podstawa ... ale ja dziś poprawiam się −.−" czytać polecenie !

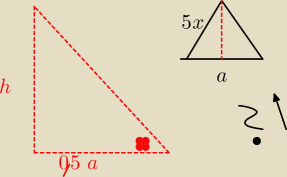Hugo: Boję sie obliczać przeciwprostokątnej troche bo nie wiem czy to tak sie da

	h
więc tgα=
	0,5a

sin²α+cos²α=1

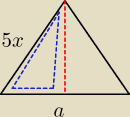Hugo: nie wiem czy tak można ale spróbuje ... z tw pitagorasa:

	6x√2
a=
	2

(0,5a)² − 25x² =h²₁

	6x√2
(		)2 − 25x2
	2

18x² −25x² h₁=√7x²

	h
sinα=
	h1

	4x
sinα=
	x√7

	4√7
sinα=
	7

Hugo: czego nie mówicie że źle

Hugo: ostatni post źle: 0,5a)²2 − 25x² =h²2₁

	6x√2
(		)2
	8

1,125x²−25x² = h²₁ h₁=√23.875x

	4√23,875
sinα=
	23,875

sinα ~ 0,81 a w odp w przyblizeniu.. tam są inne metody mają 0,88 pomózcie

Kaja: skoro |AS|=5x, a=..., to policz sobie wysokość ściany bocznej z tw. Pitagorsa

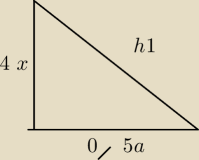Hugo: ja wiem ze tak jest w ODP ale mój sposób chyba też ma sens?! ale a rozumiesz jako co? krawędź podstawy? coś widze.... 'a' wyliczylem z tego ze podstawą jest kwadrat więc bok do przeciwprostokątnej sie ma a do a√2 czyli: 6x = a√2

	6x√2
a=		= 3x√2
	2

16x² + 0,25a² = h²₁ 16x² +0,25(3x√2)²= h²₁ 16x² +0,25*18x²= h²₁ 16x² +4,5x²= h²₁ 20,5x²=h²₁ h₁=x√20,5

Hugo: dobrze ?

	4x		40√20,5
sinα=		=
	x√20,5		205

w przyblizeniu 0,88 więc by sie wynik zgadzał !

Kaja: h₁ powinno być dobrze wyliczone. tylko sobie nie zaokrąglaj wyniku

Hugo: no wiem ale Kajo ! oni mają inny sposób wiec się w życiu nie dowiem czy dobrze a jak przybliże to wychodzi Kaja <333333333333333333333333 !

Kaja: no to ty sobie możesz sprawdzić przybliżając, ale wyniku nie podaj w przybliżeniu,zostaw jaki jest

Hugo: Wniosek? Hugo zrobił zadanie dobrze od początku tylko jak zwykle skrótować nie chlujstwo i brak systematyki i powstały blędy

Hugo: Na ile Hugo napisze mature : < ?