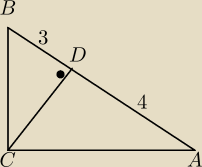
podobieństwo trójkątów mrb: Trójkąt ABC jest prostokątny. Wykaż że trójkąty ABC, ACD, CBD są podobne. Oblicz obwód trójkąta ABC,

Kaja: niech |∡CAB|=α, wtedy |∡CBA|=90−α w trójkącie CAD mamy |∡CDA|=90^o, |∡CAD|=α, |∡ACD|=180^o−(90^o+α)=90^o−α w trójkącie CDB mamy : |∡CBD|=90^o−α, |∡CDB|=90^o, |∡BCD|=180^o−(90^o+α)=90⁻α na podstawie cechy kkk wszystkie te trzy trójkąty są podobne.

|CD|		|DB
	=
|AD|		|CD|

|CD|²=3*4 |CD|=2√3 z tw. Pitagorasa |CB|²=12+9 |CB|=√21 |CA|²=12+16 |CA|=√28=2√7 obw=7+√21+2√7

5-latek: Co do wykazania ze te trojkaty sa podobne to jakie sa cechy podobienstwa trokatow? Co do obwodu CD −jest to wysokosc w tym trojkacie (pocztaj twierdzenie o wysokosci opuszczonej z wierzcholka kata prostego w trojkacie prostokatnym . Czyli CD=h=√|BD|*|DA|= √3*4=√12= 2√3 Z twierdzenia pitagorasa oblicz teraz BC i CA i praktycznie po zadaniu